题目内容
设函数f(x)是定义在(-∞,0)上的可导函数,其导函数为f′(x),且有2f(x)+xf′(x)>x2,则不等式(x+2 014)2f(x+2 014)-4f(-2)>0的解集为( )
A.(-∞,-2 012) B.(-2 012,0)
C.(-∞,-2 016) D.(-2 016,0)
C
[解析] 由2f(x)+xf′(x)>x2,x<0,得2xf(x)+x2f′(x)<x3,即[x2f(x)]′<x3<0,令F(x)=x2f(x),则当x<0时,F′(x)<0,即F(x)在(-∞,0)上是减函数.因为F(x+2 014)=(2 014+x)2·f(x+2 014),F(-2)=4f(-2),所以原不等式即为F(2 014+x)-F(-2)>0.因为F(x)在(-∞,0)上是减函数,所以由F(2 014+x)>F(-2),得2 014+x<-2,即x<-2 016,故选C.

练习册系列答案
相关题目
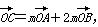
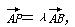 则λ=( )
则λ=( )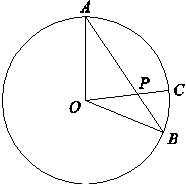
 B.
B.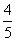
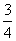 D.
D.
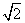 ,过点A作BC的垂线,垂足为A1,过点A1作AC的垂线,垂足为A2;过点A2作A1C的垂线,垂足为A3;…,依此类推,设BA=a1,AA1=a2,A1A2=a3,…,A5A6=a7,则a7=________.
,过点A作BC的垂线,垂足为A1,过点A1作AC的垂线,垂足为A2;过点A2作A1C的垂线,垂足为A3;…,依此类推,设BA=a1,AA1=a2,A1A2=a3,…,A5A6=a7,则a7=________.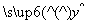 =1.23x+0.08;
=1.23x+0.08;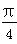 ;
;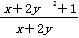 ,则x2+(y+1)2的最小值为________.
,则x2+(y+1)2的最小值为________.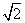 -4 B.
-4 B.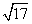 -1 C.6-2
-1 C.6-2