题目内容
(本小题满分12分)
在极坐标系中,已知圆C的圆心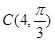 ,半径r=2,Q点在圆C上运动。
,半径r=2,Q点在圆C上运动。
(I)求圆C的极坐标方程;
(II)若P在直线OQ上运动,且OQ∶OP=3∶2,求动点P的轨迹方程。
在极坐标系中,已知圆C的圆心
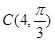 ,半径r=2,Q点在圆C上运动。
,半径r=2,Q点在圆C上运动。(I)求圆C的极坐标方程;
(II)若P在直线OQ上运动,且OQ∶OP=3∶2,求动点P的轨迹方程。
(I) ;(II)
;(II)
 ;(II)
;(II)
本试题主要考查了圆的极坐标方程的运用,以及余弦定理的综合运用。
(1) 因为圆C的圆心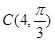 ,半径r=2,Q点在圆C上运动,由设圆C上任意一点M(r,q),则在三角形OCM中,由余弦定理得
,半径r=2,Q点在圆C上运动,由设圆C上任意一点M(r,q),则在三角形OCM中,由余弦定理得
整理得到方程。
(2)因为P在直线OQ上运动,且OQ∶OP=3∶2,设动点P(r,q),Q(r0,q0),依题意可知:
可知点Q满足的关系式得到所求的轨迹方程。
解:(I)设圆C上任意一点M(r,q),则在三角形OCM中,由余弦定理得

即:
整理即可得圆C的极坐标方程为:
(II)设P(r,q),Q(r0,q0),依题意可知:
 代入
代入 得
得
化简得:动点P的轨迹方程为:
(1) 因为圆C的圆心
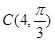 ,半径r=2,Q点在圆C上运动,由设圆C上任意一点M(r,q),则在三角形OCM中,由余弦定理得
,半径r=2,Q点在圆C上运动,由设圆C上任意一点M(r,q),则在三角形OCM中,由余弦定理得
整理得到方程。
(2)因为P在直线OQ上运动,且OQ∶OP=3∶2,设动点P(r,q),Q(r0,q0),依题意可知:

可知点Q满足的关系式得到所求的轨迹方程。
解:(I)设圆C上任意一点M(r,q),则在三角形OCM中,由余弦定理得


即:

整理即可得圆C的极坐标方程为:

(II)设P(r,q),Q(r0,q0),依题意可知:
 代入
代入 得
得
化简得:动点P的轨迹方程为:


练习册系列答案
相关题目
 ,
,


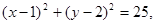

 取何实数,直线
取何实数,直线 与圆C恒相交;
与圆C恒相交; 过点A(3,1),且过点P(4,4)的直线PF与圆C相切并和x轴的负半轴相交于点F.
过点A(3,1),且过点P(4,4)的直线PF与圆C相切并和x轴的负半轴相交于点F. 的取值范围.
的取值范围.
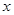 轴的正半轴为极轴,并在两种坐标系中取相同的长度单位.已知直线的极坐标方程为
轴的正半轴为极轴,并在两种坐标系中取相同的长度单位.已知直线的极坐标方程为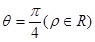 ,它与曲线
,它与曲线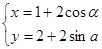 (
(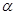 为参数)相交于两点A和B,则|AB|=______.
为参数)相交于两点A和B,则|AB|=______.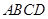 的两条对角线相交于点
的两条对角线相交于点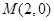 ,
,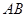 边所在直线的方程为
边所在直线的方程为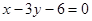 ,点
,点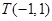 在
在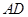 边所在直线上。
边所在直线上。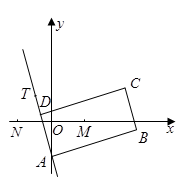
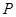 过点
过点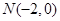 ,且与矩形
,且与矩形 与圆
与圆 相切,且与直线
相切,且与直线
 平行,则直线
平行,则直线 上的点到直线
上的点到直线 的最近距离是
的最近距离是 被圆
被圆 截得的弦长为
截得的弦长为
