题目内容
13.已知数列{an}的前n项和Sn=2n2-19n+1,记Tn=|a1|+|a2|+…+|an|.(1)求Sn的最小值及相应n的值;
(2)求Tn.
分析 (1)Sn=2n2-19n+1=2$(n-\frac{19}{4})^{2}$-$\frac{353}{8}$,利用二次函数的单调性即可得出.
(2)由Sn=2n2-19n+1,n=1时,a1=-16.n≥2时,an=Sn-Sn-1=4n-21.由an≤0,解得n≤5.n≥6时,an>0.可得n≤5时,Tn=|a1|+|a2|+…+|an|=-(a1+a2+…+an)=-Sn.n≥6时,Tn=-(a1+a2+…+a5)+a6+…+an=-2S5+Sn.
解答 解:(1)Sn=2n2-19n+1=2$(n-\frac{19}{4})^{2}$-$\frac{353}{8}$,
∴n=5时,Sn取得最小值=-44.
(2)由Sn=2n2-19n+1,
∴n=1时,a1=2-19+1=-16.
n≥2时,an=Sn-Sn-1=2n2-19n+1-[2(n-1)2-19(n-1)+1]=4n-21.
由an≤0,解得n≤5.n≥6时,an>0.
∴n≤5时,Tn=|a1|+|a2|+…+|an|=-(a1+a2+…+an)=-Sn=-2n2+19n-1.
n≥6时,Tn=-(a1+a2+…+a5)+a6+…+an
=-2S5+Sn
=2n2-19n+89.
∴Tn=$\left\{\begin{array}{l}{-2{n}^{2}+19n-1,1≤n≤5}\\{2{n}^{2}-19n+89,n≥6}\end{array}\right.$.
点评 本题考查了等差数列的通项公式及其前n项和公式、不等式的解法、绝对值数列求和问题,考查了分类讨论方法推理能力与计算能力,属于中档题.

练习册系列答案
 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
18.圆(x-2)2+y2=5与直线y=2x+1的位置关系是( )
| A. | 相交 | B. | 相切 | C. | 相离 | D. | 直线过圆心 |
5.若函数f(x)=x(lnx-ax)在区间(0,e)上有两个不同的极值点,则实数a的取值范围是( ) (e是自然对数的底数)
| A. | $(\frac{1}{2e},\frac{1}{2})$ | B. | $(0,\frac{1}{2})$ | C. | $(\frac{1}{2e},+∞)$ | D. | $(\frac{1}{e},\frac{1}{2})$ |
3.$\frac{7}{16}$-$\frac{7}{8}$sin215°的值为( )
| A. | $\frac{7}{32}$ | B. | $\frac{7\sqrt{3}}{32}$ | C. | $\frac{7}{16}$ | D. | $\frac{7\sqrt{3}}{16}$ |
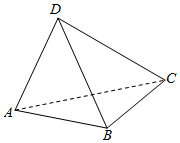 如图,在三棱锥D-ABC中,已知AB=2,$\overrightarrow{AC}$•$\overrightarrow{BD}$=-3,设AD=a,BC=b,CD=c,则$\frac{c^2}{ab+1}$的最小值为2.
如图,在三棱锥D-ABC中,已知AB=2,$\overrightarrow{AC}$•$\overrightarrow{BD}$=-3,设AD=a,BC=b,CD=c,则$\frac{c^2}{ab+1}$的最小值为2.