题目内容
如图,设P是圆x2+y2=25上的动点,点D是P在x轴上的投影,M为PD上一点,且|MD|=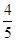 |PD|,当P在圆上运动时,求点M的轨迹C的方程。
|PD|,当P在圆上运动时,求点M的轨迹C的方程。
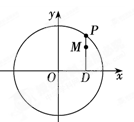
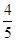 |PD|,当P在圆上运动时,求点M的轨迹C的方程。
|PD|,当P在圆上运动时,求点M的轨迹C的方程。
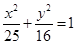
试题分析:这是一道典型的关于轨迹问题的题目,通常的解法:①设出所求轨迹点的坐标;②找出已知点的坐标与其之间的等量关系;③代入已知点的轨迹方程;④求出所求点的轨迹方程.在此题的解答过程中,可以先设出所求点
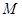 的坐标
的坐标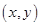 ,已知点
,已知点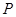 的坐标
的坐标 ,由“点
,由“点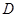 是
是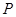 在
在 轴上的投影”且“
轴上的投影”且“ ”得到点
”得到点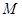 与点
与点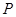 坐标之间的等量关系
坐标之间的等量关系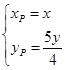 ,又由于点
,又由于点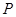 是已知圆上的点,将其坐标代入圆方程,经整理即可得到所点
是已知圆上的点,将其坐标代入圆方程,经整理即可得到所点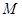 的轨迹方程.
的轨迹方程.试题解析:设
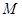 的坐标为
的坐标为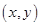 ,
,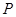 的坐标为
的坐标为 ,则由已知得
,则由已知得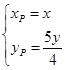 5分
5分因为点
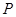 在圆上,所以
在圆上,所以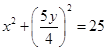 ,即所求点
,即所求点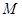 的轨迹
的轨迹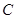 的方程为
的方程为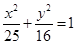 . 10分
. 10分
练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
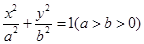 的离心率为
的离心率为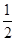 ,且经过点
,且经过点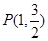 . 过它的两个焦点
. 过它的两个焦点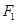 ,
,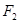 分别作直线
分别作直线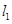 与
与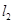 ,
,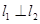 .
.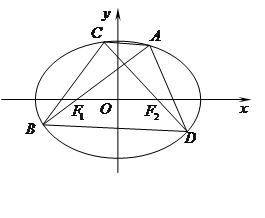
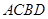 的面积
的面积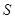 的取值范围.
的取值范围. 为焦点在
为焦点在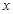 轴上的椭圆,则实数
轴上的椭圆,则实数 ,
, 满足( )
满足( )



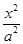 +
+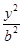 =1(a>b>0)的左右焦点,P是椭圆上一点,∠F1PF2=90°,求椭圆离心率的最小值为
=1(a>b>0)的左右焦点,P是椭圆上一点,∠F1PF2=90°,求椭圆离心率的最小值为 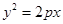 与椭圆
与椭圆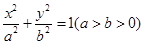 有相同的焦点
有相同的焦点 ,
,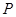 是两曲线的公共点,若
是两曲线的公共点,若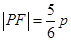 ,则此椭圆的离心率为 .
,则此椭圆的离心率为 .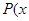 、
、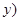 是曲线
是曲线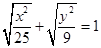 上的点,
上的点,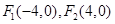 ,则必有 ( )
,则必有 ( )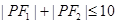



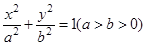 的左、右焦点分别为
的左、右焦点分别为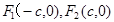 ,若椭圆上存在点P使
,若椭圆上存在点P使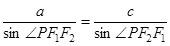 ,则该椭圆的离心率的取值范围为___
,则该椭圆的离心率的取值范围为___ 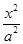 +
+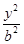 =1(a>b>0)上一点,且
=1(a>b>0)上一点,且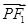 ·
·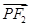 =0,tan∠PF1F2=
=0,tan∠PF1F2=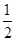 则此椭圆的离心率e=( )
则此椭圆的离心率e=( )

