题目内容
14.过正方体ABCD-A1B1C1D1的顶点A作直线l,使l与直线AD1所成的角为30°,且与平面C1D1C所成的角为60°,则这样的直线l的条数是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 在平面C1D1C内,以点D为圆心,半径为$\frac{\sqrt{3}}{3}$AD画圆,则点A与此圆上的点的连线满足:与平面C1D1C所成的角为60°,即可得出结论.
解答  解:在平面C1D1C内,以点D为圆心,半径为$\frac{\sqrt{3}}{3}$AD画圆,则点A与此圆上的点的连线满足:与平面C1D1C所成的角为60°.
解:在平面C1D1C内,以点D为圆心,半径为$\frac{\sqrt{3}}{3}$AD画圆,则点A与此圆上的点的连线满足:与平面C1D1C所成的角为60°.
所以满足l与直线AD1所成的角为30°有且只有2条,
故选:B.
点评 本题考查空间直线与直线,直线与平面所成角,考查学生分析解决问题的能力,有难度.

练习册系列答案
相关题目
9.设x∈{-1,1},y∈{-2,0,2},则以(x,y)为坐标的点落在不等式x+2y≥1所表示的平面区域内的概率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{4}$ |
6.已知平面内三点A,B,C满足|$\overrightarrow{AB}$|=|$\overrightarrow{CA}$|=1,|$\overrightarrow{BC}$|=$\sqrt{3}$,则$\overrightarrow{AB}$•$\overrightarrow{BC}$为( )
| A. | $\frac{3}{2}$ | B. | -$\frac{3}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
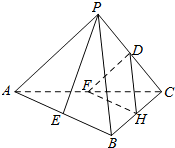 如图,在三棱锥P-ABC中,E、F、G、H分别是AB、AC、PC、BC的中点,且PA=PB,AC=BC.
如图,在三棱锥P-ABC中,E、F、G、H分别是AB、AC、PC、BC的中点,且PA=PB,AC=BC.