��Ŀ����
13����ֱ������ϵxOy�У�ֱ��l�ķ���Ϊx-y-4=0������C�IJ�������Ϊ$\left\{\begin{array}{l}x=\sqrt{3}cos��\\ y=sin��\end{array}\right.$����1����֪�ڼ�����ϵ����ֱ������ϵxOyȡ��ͬ�ij��ȵ�λ������ԭ��OΪ���㣬��x��������Ϊ���ᣩ�У���P�ļ�����Ϊ$��4��\frac{��}{2}��$�������P����ֱ��l��ֱ��ֱ�߷���
��2�����Q������C�ϵ�һ�����㣬������ֱ��l�ľ������Сֵ��
���� ��1���ڼ�����ϵ�У����ȵ�P�ļ�����Ϊ$��4��\frac{��}{2}��$��ת��Ϊֱ������ΪP��0��4������һ�����ֱ��l�ķ���Ϊx-y-4=0��б��Ϊ1���������ֱ�ߴ�ֱ�ij�Ҫ���������Ӧ��ֱ�߷���x+y-4=0��
��2��������Q��$\sqrt{3}cos��$��sin����Ϊ����C�ϵĶ��㣬ֱ�����õ㵽ֱ��x-y-4=0�ľ��빫ʽ�����������Ǻ����ĺ�ȱ任�����Ӧ�Ľ����
��� �⣺��1���ڼ�����ϵ�У���P�ļ�����Ϊ$��4��\frac{��}{2}��$��ת��Ϊֱ������ΪP��0��4����
ֱ��l�ķ���Ϊx-y-4=0��б��Ϊ1��
����P����ֱ��l��ֱ��ֱ�߷���Ϊ��y-4=-x��
�����ã�x+y-4=0��
��2����Q��$\sqrt{3}cos��$��sin����Ϊ����C�ϵĶ��㣬
��ֱ��l��x-y-4=0�ľ��룺
d=$\frac{|\sqrt{3}cos��+sin��-4|}{\sqrt{2}}$��
=$\frac{|2sin����+\frac{��}{3}��-4|}{\sqrt{2}}$��
��$��=\frac{��}{6}$ʱ��${d}_{min}=\sqrt{2}$��
���� ���⿼���֪ʶҪ�㣺�������ֱ������Ļ�����ֱ�ߴ�ֱ�ij�Ҫ������ֱ�߷��̵����㵽ֱ�ߵľ��빫ʽ��Ӧ�ã����Ǻ�����ϵʽ�ĺ�ȱ任�����Ǻ�������ֵ�����ڻ������ͣ�

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�| A�� | -$\frac{3\sqrt{3}}{2}$ | B�� | -$\frac{3}{2}$ | C�� | $\frac{3}{2}$ | D�� | $\frac{3\sqrt{3}}{2}$ |
| A�� | a��-3 | B�� | a��-3 | C�� | a��5 | D�� | a��3 |
| A�� | b��d��a��c | B�� | d��b��c��a | C�� | b��d��c��a | D�� | d��b��a��c |
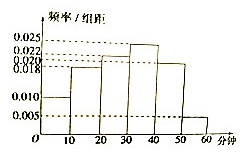 ���Ӵ�ý��˾Ϊ�˽�ij�������ӹ��ڶ���Լ���˻����������������ȡ��100�����ڽ��е��飬����Ů����55���������Ǹ��ݵ��������ƵĹ����վ��տ���������Ŀʱ���Ƶ�ʷֲ�ֱ��ͼ��
���Ӵ�ý��˾Ϊ�˽�ij�������ӹ��ڶ���Լ���˻����������������ȡ��100�����ڽ��е��飬����Ů����55���������Ǹ��ݵ��������ƵĹ����վ��տ���������Ŀʱ���Ƶ�ʷֲ�ֱ��ͼ�����վ��տ���������Ŀʱ�䲻����40���ӵĹ��ڳ�Ϊ�������ԡ�����֪�������ԡ�����10��Ů�ԣ�
��1�����������ԡ��е����Թ���������
��2���ݴ��������2��2�����������Ƿ���Ϊ�������ԡ����Ա��йأ�
| P��K2��k�� | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
���ο���ʽ��${K^2}=\frac{{n{{��ad-bc��}^2}}}{��a+b����c+d����a+c����b+d��}������n=a+b+c+d$
| �������� | ������ | �ϼ� | |
| �� | |||
| Ů | |||
| �ϼ� |