题目内容
已知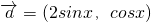 ,
,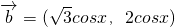 ,且
,且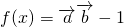 .
.
(1)求函数f(x)的最小正周期及单调增区间;
(2)若 ,求函数f(x)的最大值与最小值.
,求函数f(x)的最大值与最小值.
解:(1)因为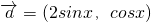 ,
,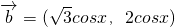 ,
,
所以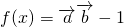 =
=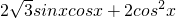 -1=
-1= =2sin(2x
=2sin(2x ).
).
所以f(x)的最小正周期为T= ,由2kπ-
,由2kπ-
 2kπ
2kπ ,k∈Z解得
,k∈Z解得
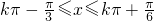 ,即单调递增区间为[
,即单调递增区间为[ ,
,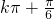 ]k∈Z
]k∈Z
(2)由(1)可知f(x)在区间[0, ]上单调递增,在[
]上单调递增,在[ ,
, ]上单调递减,
]上单调递减,
故当x= 时,f(x)取到最大值f(
时,f(x)取到最大值f( )=2;当x=
)=2;当x= 时,f(x)取到最大值f(
时,f(x)取到最大值f( )=-1.
)=-1.
分析:(1)由三角函数公式可得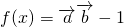 =
=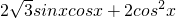 -1=
-1= =2sin(2x
=2sin(2x )由此可求解,
)由此可求解,
(2)利用(1)的结论可知函数在给定区间[0, ]上的单调性,即可获得最大最小值.
]上的单调性,即可获得最大最小值.
点评:本题为三角函数与向量的综合应用,准确记住公式是解决问题的关键,属中档题.
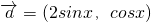 ,
,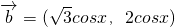 ,
,所以
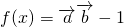 =
=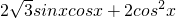 -1=
-1= =2sin(2x
=2sin(2x ).
).所以f(x)的最小正周期为T=
 ,由2kπ-
,由2kπ-
 2kπ
2kπ ,k∈Z解得
,k∈Z解得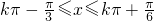 ,即单调递增区间为[
,即单调递增区间为[ ,
,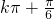 ]k∈Z
]k∈Z(2)由(1)可知f(x)在区间[0,
 ]上单调递增,在[
]上单调递增,在[ ,
, ]上单调递减,
]上单调递减,故当x=
 时,f(x)取到最大值f(
时,f(x)取到最大值f( )=2;当x=
)=2;当x= 时,f(x)取到最大值f(
时,f(x)取到最大值f( )=-1.
)=-1.分析:(1)由三角函数公式可得
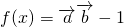 =
=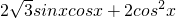 -1=
-1= =2sin(2x
=2sin(2x )由此可求解,
)由此可求解,(2)利用(1)的结论可知函数在给定区间[0,
 ]上的单调性,即可获得最大最小值.
]上的单调性,即可获得最大最小值.点评:本题为三角函数与向量的综合应用,准确记住公式是解决问题的关键,属中档题.

练习册系列答案
相关题目
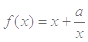 ,且
,且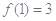 .
. 的值,并确定函数
的值,并确定函数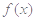 的定义域;
的定义域;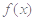 在
在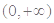 范围内的单调性;
范围内的单调性;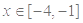 时,求出函数
时,求出函数 ,
, ,且
,且 .
. 的值;
的值; .
. ,且
,且 .
.
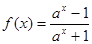 (
(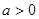 且
且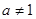 )
) 的定义域和值域
的定义域和值域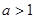 时,若对任意实数
时,若对任意实数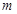 ,不等式
,不等式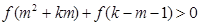 恒成立,求实数
恒成立,求实数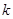 的取值范围
的取值范围