题目内容
20.如图(1)ABCD为梯形,AB∥CD,∠C=60°,点E在CD上,AB=CE,$BF=\frac{1}{3}BD=\sqrt{3}$,BD⊥BC.现将△ADE沿AE折成如图(2)△APE位置,使得二面角P-AE-C的大小为$\frac{π}{3}$.
(Ⅰ)求PB的长度;
(Ⅱ)求证:PB⊥平面ABCE;
(Ⅲ)求直线CE与平面APE所成角的正弦值.
分析 (Ⅰ)由已知可得BC∥AE,再由BF⊥BC,得BF⊥AE,进一步得到∠PFB为二面角P-AE-C的平面角为60°,在△BFP中,利用余弦定理求得BP;
(Ⅱ)由勾股定理可知BF⊥PB,再由线面垂直的判定和性质可得AE⊥PB,则有PB⊥平面ABCE;
(Ⅲ)法一、作BN⊥PF于N点,连AN,由(Ⅱ)可知,AE⊥面BFP,得面BFP⊥面APE,进一步可得BN⊥面APE,则∠BAN是直线AB与平面APE所成的角,求解三角形得答案;
法二、由于BF,BP,BC两两互相垂直,如图,建立空间直角坐标系,求出所用点的坐标,得到平面APE的一个法向量$\overrightarrow{n}$,再求出$\overrightarrow{AB}$的坐标,由向量$\overrightarrow{n}$与$\overrightarrow{AB}$所成角的余弦值可得直线CE与平面APE所成角的正弦值.
解答 解:(Ⅰ)∵AB∥EC,AB=EC,∴四边形ABCE是平行四边形,则BC∥AE,
又∵BF⊥BC,∴BF⊥AE,
∴AE⊥FB,AE⊥FP,即∠PFB为二面角P-AE-C的平面角为60°,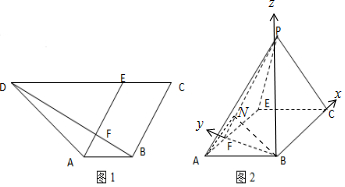
又$BF=\sqrt{3},PF=2\sqrt{3}$,由余弦定理BP2=BF2+PF2-2BF•PFcos∠BFP=9,
得BP=3;
证明:(Ⅱ)∵$BF=\sqrt{3},PF=2\sqrt{3}$,
BP=3,满足BF2+BP2=PF2,∴BF⊥PB.
又∵BF⊥AE,PF⊥AE,且BF∩PF=F,
∴AE⊥面PFB,则AE⊥PB,
而BF∩AE=F,∴PB⊥平面ABCE;
解:(Ⅲ)法一、作BN⊥PF于N点,连AN,
由(Ⅱ)可知,AE⊥面BFP,∴面BFP⊥面APE,
又面BFP∩面APE=PF,∴BN⊥面APE,则∠BAN是直线AB与平面APE所成的角.
在直角三角形FBP中,BN=BF•sin60°=$\frac{3}{2}$,∴sin∠NAB=$\frac{BN}{AB}$=$\frac{\frac{3}{2}}{2}=\frac{3}{4}$.
∴直线AB与平面APE所成角的正弦值为$\frac{3}{4}$.
∵AB∥CE,
∴直线CE与平面APE所成角的正弦值为$\frac{3}{4}$;
法二、由于BF,BP,BC两两互相垂直,如图,建立空间直角坐标系,
则$B(0,0,0),C(3,0,0),A(-1,\sqrt{3},0),E(2,\sqrt{3},0),P(0,0,3)$,
设平面APE的法向量为$\overrightarrow n=(x,y,z)$,
由$\left\{{\begin{array}{l}{\overrightarrow n•\overrightarrow{AE}=0}\\{\overrightarrow n•\overrightarrow{AP}=0}\end{array}}\right.$,得$\left\{{\begin{array}{l}{(x,y,z)•(3,0,0)=0}\\{(x,y,z)•(1,-\sqrt{3},3)=0}\end{array}}\right.$,即$\left\{{\begin{array}{l}{x=0}\\{x-\sqrt{3}y+3z=0}\end{array}}\right.$,取z=1,得$\overrightarrow n=(0,\sqrt{3},1)$,
设直线AB与平面APE所成的角为θ,$\overrightarrow{AB}=(1,-\sqrt{3},0)$,
则sinθ=|cos<$\overrightarrow{n},\overrightarrow{AB}$>|=$\frac{|\overrightarrow{n}•\overrightarrow{AB}|}{|\overrightarrow{n}|•|\overrightarrow{AB}|}=\frac{|-3|}{2×2}=\frac{3}{4}$,
故直线AB与平面APE所成角的正弦值为$\frac{3}{4}$,
∵AB∥CE,
∴直线CE与平面APE所成角的正弦值为$\frac{3}{4}$.
点评 本题考查直线与平面垂直的判定,考查空间想象能力和思维能力,训练了利用空间向量求解线面角,是中档题.

 考前必练系列答案
考前必练系列答案| A. | 向左平移$\frac{π}{4}$个单位长度,再把所得各点的横坐标缩短到原来的$\frac{1}{3}$倍 (纵坐标不变) | |
| B. | 向右平移$\frac{π}{4}$个单位长度,再把所得各点的横坐标缩短到原来的$\frac{1}{3}$倍(纵坐标不变) | |
| C. | 向左平移$\frac{π}{4}$个单位长度,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变) | |
| D. | 向右平移$\frac{π}{4}$个单位长度,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变) |

若输入5,则程序运行的结果为( )
| A. | 1 | B. | 10 | C. | 25 | D. | 26 |
| A. | 35种 | B. | 70种 | C. | 210种 | D. | 105种 |
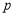 :对任意
:对任意 ,
,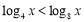 ,命题
,命题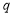 :存在
:存在 ,使得
,使得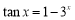 ,则下列命题为真命题的是( )
,则下列命题为真命题的是( )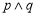 B.
B.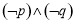
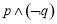 D.
D.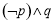
 (
( )的图象如图所示,在下列结论中:①
)的图象如图所示,在下列结论中:① ;②
;② ;③b=-2a;④
;③b=-2a;④ ,正确结论的个数是( )
,正确结论的个数是( )