题目内容
若cos(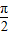 -α)-cos(2π-α)=
-α)-cos(2π-α)= ,α是第二象限的角,则tanα= .
,α是第二象限的角,则tanα= .
【答案】分析:依题意,可知sinα-cosα= ,结合题意可求得sinα=
,结合题意可求得sinα= ,cosα=-
,cosα=- ,从而可求得tanα.
,从而可求得tanα.
解答:解:∵cos(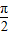 -α)=sinα,cos(2π-α)=cosα,
-α)=sinα,cos(2π-α)=cosα,
∴cos(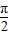 -α)-cos(2π-α)=
-α)-cos(2π-α)= ?sinα-cosα=
?sinα-cosα= ,①
,①
∴两端平方得:1-sin2α=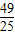 ,
,
∴sin2α=-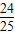 ,
,
∴1+sin2α=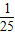 ,即(sinα+cosα)2=
,即(sinα+cosα)2=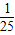 ②
②
∵sinα-cosα=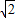 sin(α-
sin(α-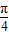 )=
)= ,
,
∴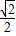 <sin(α-
<sin(α-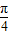 )=
)=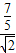 <1,又α是第二象限的角,
<1,又α是第二象限的角,
∴2kπ+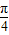 <α-
<α-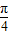 <2kπ+
<2kπ+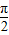 ,
,
∴2kπ+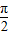 <α<2kπ+
<α<2kπ+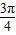 ,k∈Z.
,k∈Z.
∴|sinα|=sinα>|cosα|.
∴sinα+cosα>0
由②得:sinα+cosα= ③
③
联立①③得:sinα= ,cosα=-
,cosα=- ,
,
∴tanα=- .
.
故答案为:- .
.
点评:本题考查三角函数的诱导公式,考查二倍角公式,考查方程思想与转化思想、抽象思维与运算能力,求得sinα= ,cosα=-
,cosα=- 是关键,也是难点,属于中档题.
是关键,也是难点,属于中档题.
 ,结合题意可求得sinα=
,结合题意可求得sinα= ,cosα=-
,cosα=- ,从而可求得tanα.
,从而可求得tanα.解答:解:∵cos(
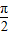 -α)=sinα,cos(2π-α)=cosα,
-α)=sinα,cos(2π-α)=cosα,∴cos(
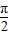 -α)-cos(2π-α)=
-α)-cos(2π-α)= ?sinα-cosα=
?sinα-cosα= ,①
,①∴两端平方得:1-sin2α=
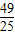 ,
,∴sin2α=-
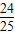 ,
,∴1+sin2α=
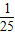 ,即(sinα+cosα)2=
,即(sinα+cosα)2=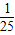 ②
②∵sinα-cosα=
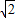 sin(α-
sin(α-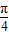 )=
)= ,
,∴
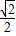 <sin(α-
<sin(α-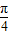 )=
)=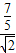 <1,又α是第二象限的角,
<1,又α是第二象限的角,∴2kπ+
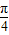 <α-
<α-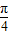 <2kπ+
<2kπ+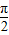 ,
,∴2kπ+
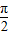 <α<2kπ+
<α<2kπ+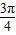 ,k∈Z.
,k∈Z.∴|sinα|=sinα>|cosα|.
∴sinα+cosα>0
由②得:sinα+cosα=
 ③
③联立①③得:sinα=
 ,cosα=-
,cosα=- ,
,∴tanα=-
 .
.故答案为:-
 .
.点评:本题考查三角函数的诱导公式,考查二倍角公式,考查方程思想与转化思想、抽象思维与运算能力,求得sinα=
 ,cosα=-
,cosα=- 是关键,也是难点,属于中档题.
是关键,也是难点,属于中档题. 
练习册系列答案
相关题目
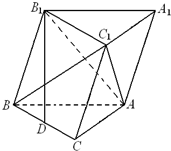 已知斜三棱柱ABC-A1B1C1的底面是直角三角形,∠ACB=90°,侧棱与底面所成角为θ,点B1在底面上的射影D落在BC上.
已知斜三棱柱ABC-A1B1C1的底面是直角三角形,∠ACB=90°,侧棱与底面所成角为θ,点B1在底面上的射影D落在BC上.