题目内容
判断下列各组中的两个函数是同一函数的为( )
(1) ,
, ;
;
(2) ,
, ;
;
(3) ,
, ;
;
(4) ,
, .
.
| A.(1),(4) | B.(2),(3) | C.(1) | D.(3) |
A
解析试题分析:对于A,由于函数 的定义域为
的定义域为 ,同时解析式化简为f(x)=x-3而函数
,同时解析式化简为f(x)=x-3而函数 于其定义域同,对应法则同,因此事同一函数。
于其定义域同,对应法则同,因此事同一函数。
对于B,由于 中
中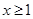 ,而
,而 中
中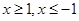 定义域不同,不成立。
定义域不同,不成立。
对于C,由于 ,
, =
= ,明显对应法则不同,不成立。
,明显对应法则不同,不成立。
对于D,由于 ,
, =x,定义域同,对应法则同故成立。故选A.
=x,定义域同,对应法则同故成立。故选A.
考点:考查同一函数的概念。
点评:解决该试题关键是理解,同一函数的两个条件:定义域相同,对应法则相同即可。因此结合概念进行逐一判定,属于基础题。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
下列函数中,在区间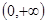 为增函数的是( )
为增函数的是( )
A.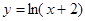 | B.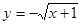 | C. | D.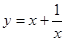 |
下列函数中,值域是 的函数为
的函数为
A. | B. |
C. | D. |
三个数 ,
,  ,
,  的大小顺序为 ( )
的大小顺序为 ( )
A. | B. |
C.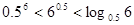 | D. |
若定义在R上的偶函数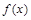 对任意
对任意
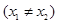 ,有
,有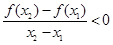 ,则
,则
A.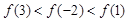 | B.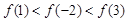 |
C.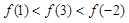 | D. |
已知函数 在
在 上是增函数,
上是增函数, ,若
,若 ,则
,则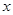 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
对于定义域为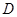 的函数
的函数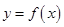 和常数
和常数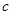 ,若对任意正实数
,若对任意正实数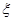 ,
,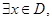 使得
使得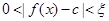 恒成立,则称函数
恒成立,则称函数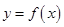 为“敛
为“敛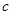 函数”.现给出如下函数:
函数”.现给出如下函数:
①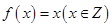 ; ②
; ②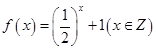 ;
;
③ 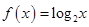 ; ④
; ④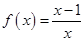 .
.
其中为“敛1函数”的有
| A.①② | B.③④ | C.②③④ | D.①②③ |
设 是定义在R上的奇函数,当
是定义在R上的奇函数,当 时,
时, ,则
,则 的值是 ( )
的值是 ( )
A. | B. | C.1 | D.3 |

