题目内容
设 是定义在R上的奇函数,当
是定义在R上的奇函数,当 时,
时, ,则
,则 的值是 ( )
的值是 ( )
A. | B. | C.1 | D.3 |
A
解析试题分析:因为函数为奇函数,所以f(1)=-f(-1)=-[2-(-1)]=-3,故选A。
考点:本题主要考查分段函数的概念,函数的奇偶性。
点评:简单题,理解函数的奇偶性,f(1)=-f(-1).

练习册系列答案
相关题目
判断下列各组中的两个函数是同一函数的为( )
(1) ,
, ;
;
(2) ,
, ;
;
(3) ,
, ;
;
(4) ,
, .
.
| A.(1),(4) | B.(2),(3) | C.(1) | D.(3) |
函数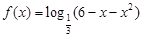 的单调递增区间是
的单调递增区间是
A. | B. | C. | D. |
已知函数 的定义域为R,当
的定义域为R,当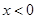 时,
时, ,且对任意的实数
,且对任意的实数 R,等式
R,等式 成立.若数列
成立.若数列 满足
满足 ,且
,且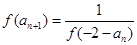 (
( ),则
),则 的值为( )
的值为( )
| A.4024 | B.4023 | C.4022 | D.4021 |
已知-2<x<0,则 的最小值为( )
的最小值为( )
| A.2 | B.3 | C. | D.-2 |
函数 的零点所在的区间是( )
的零点所在的区间是( )
A. | B. | C. | D. |
若定义 上的函数
上的函数 满足:对于任意
满足:对于任意

 且当
且当 时有
时有 ,若
,若 的最大值、最小值分别为M,N,M+N等于( )
的最大值、最小值分别为M,N,M+N等于( )
| A.2011 | B.2012 | C.4022 | D.4024 |
已知函数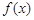 满足:①定义域为R;②
满足:①定义域为R;② ,有
,有 ;③当
;③当 时,
时, .记
.记 .根据以上信息,可以得到函数
.根据以上信息,可以得到函数 的零点个数为 ( )
的零点个数为 ( )
| A.15 | B.10 |
| C.9 | D.8 |
函数 的零点所在的一个区间是
的零点所在的一个区间是
A. | B. | C. | D. |