题目内容
【题目】已知数列
满足： 
， 
， 
.
（1）证明： 
；
（2）证明： 
；
（3）证明： 
.
【答案】(1)证明见解析；(2)证明见解析；(3)证明见解析.
【解析】试题分析：（1）先用数学归纳法证明
，再设
， 
，求出
的单调性，即可得证；（2）要证
，只需证
，令
， 
，求出
的单调性，推出
，再令
， 
，求出
的单调性，推出
，即可得证；（3）由（2）可得
，由迭代可得
，再根据
，推出
，然后由
，推出
，即可得证.
试题解析：（1）先用数学归纳法证明
.
①当
时，∵
，∴
；
②假设当
时， 
，则当
时， 
.
由①②可知
.
再证
.
，
令
， 
，则
，
所以
在
上单调递减，所以
，
所以
，即
.
（2）要证
，只需证
，
只需证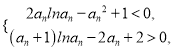
其中
，
先证
，
令
， 
，只需证
.
因为
，
所以
在
上单调递减，所以
.
再证
，
令
， 
，只需证
，
，
令
， 
，则
，
所以
在
上单调递增，所以
，
从而
，所以
在
上单调递增，所以
，
综上可得
.
（3）由（2）知，一方面， 
，由迭代可得
，
因为
，所以
，所以
；
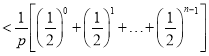
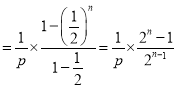另一方面，即
，
由迭代可得
.
因为
，所以
，所以
；
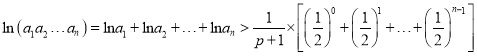
综上， 
.
练习册系列答案
相关题目
