题目内容
11．与圆C：x2+y2-2x-35=0关于直线y=-x对称的圆的方程为（ ）| A． | （x-1）2+y2=36 | B． | （x+1）2+y2=36 | C． | x2+（y+1）2=36 | D． | x2+（y-1）2=36 |
分析 求出已知圆的圆心坐标与半径，然后求出对称圆的圆心与半径，即可求出对称圆的方程．
解答 解：圆C：x2+y2-2x-35=0的圆心坐标为（1，0），半径为6，
圆圆C：x2+y2-2x-35=0关于直线y=-x对称的圆的圆心坐标（0，-1），
所以圆圆C：x2+y2-2x-35=0关于直线y=-x对称的圆的方程为x2+（y+1）2=36．
故选C．
点评 本题考查关于点、直线对称的圆的方程的求法，考查计算能力．
练习册系列答案
相关题目
19．
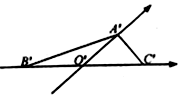已知水平放置的△A BC是按“斜二测画法”得到如图所示的直观图，其中 B'O'=C'O'=1，${A}'{O}'=\frac{{\sqrt{3}}}{2}$，那么对于原△ABC则有（ ）
已知水平放置的△A BC是按“斜二测画法”得到如图所示的直观图，其中 B'O'=C'O'=1，${A}'{O}'=\frac{{\sqrt{3}}}{2}$，那么对于原△ABC则有（ ）| A． | AB=BC | B． | AB=BC，且AB⊥BC | C． | AB⊥BC | D． | AB=AC，且AB⊥AC |
