题目内容
已知p:{x|1-c<x<1+c,c>0},q:(x-3)2<16,且p是q的充分而不必要条件,求c的取值范围.
考点:必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:对于q:(x-3)2<16,解得-1<x<7.由于p是q的充分而不必要条件,可得(1-c,1+c)?(-1,7),(c>0).解出即可.
解答:
解:p:{x|1-c<x<1+c,c>0},
q:(x-3)2<16,解得-1<x<7.
∵p是q的充分而不必要条件,
∴(1-c,1+c)?(-1,7),(c>0).
∴
,解得0<c≤2.
∴c的取值范围是(0,2].
q:(x-3)2<16,解得-1<x<7.
∵p是q的充分而不必要条件,
∴(1-c,1+c)?(-1,7),(c>0).
∴
|
∴c的取值范围是(0,2].
点评:本题考查了简易逻辑的有关知识、不等式的解法,考查了推理能力,属于基础题.

练习册系列答案
相关题目
在平行四边形ABCD中,AB=4,AD=2,E,F分别是BC,CD的中点,且
•
=-15,则∠ABC=( )
| DE |
| BF |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知定义在[1-2a,2-a]上的偶函数f(x),当x≥0时,f(x)=x+ex,若f(t)<f(2t-1).则t的取值范围是( )
| A、[-1,1] | ||
| B、[0,1] | ||
C、[
| ||
D、[0,
|
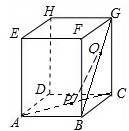 如图,正方体ABCD-EFGH的棱长为a,点P在AC上,点Q在BG上,AP=BQ=a,求证:PQ⊥AD.
如图,正方体ABCD-EFGH的棱长为a,点P在AC上,点Q在BG上,AP=BQ=a,求证:PQ⊥AD. 如图,已知PA⊥平面ABC,AD⊥BC于D,BC=CD=AD=1.记∠BPC=θ,则当PD=
如图,已知PA⊥平面ABC,AD⊥BC于D,BC=CD=AD=1.记∠BPC=θ,则当PD=