题目内容
【题目】在△ABC中，a，b，c分别是内角A，B，C的对边，AB=5，cos∠ABC= 
． 
（1）若BC=4，求△ABC的面积S△ABC；
（2）若D是边AC的中点，且BD= 
，求边BC的长．
【答案】
（1）解： 
，BC=4，
又∠ABC∈（0，π），所以 
，
∴ 
（2）解：以BA，BC为邻边作如图所示的平行四边形ABCE，如图，
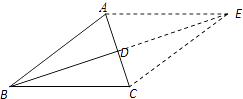
则 
，BE=2BD=7，CE=AB=5，
在△BCE中，由余弦定理：BE2=CB2+CE2﹣2CBCEcos∠BCE．
即 
，
解得：CB=4
【解析】（1） 先求sin∠ABC，从而 
；（2） 以BA，BC为邻边作如图所示的平行四边形ABCE，求出cos∠BCF，BE，CE，从而由余弦定理可得 ，可解CB的值．
【考点精析】掌握余弦定理的定义是解答本题的根本，需要知道余弦定理:
;
;
．
练习册系列答案
中考解读考点精练系列答案
各地期末复习特训卷系列答案
相关题目
