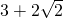Question

当点（x，y）在直线x+3y=2上移动时，z=3^x+27^y+3的最小值是（　　）

• A．

  8

  3

• B．3+2

  2

• C．6
• D．9

Answer 1

分析：由x+3y=2可得z=3^x+27^y+3=3^2-3y+27^y+3=

9

27y

+27y+3，利用基本不等式可求函数的最小值

解答：解：∵x+3y=2
∴z=3^x+27^y+3=3^2-3y+27^y+3=

9

27y

+27y+3≥2

9 27y •27y

+3=9
当且仅当

9

27y

=27y即27^y=3，y=

1

3

时取等号
∴Z的最小值为9
故选：D

点评：本题主要考查了基本不等式在求解函数的最小值中的应用，属于基础试题