题目内容
15.圆(x+2)2+y2=4与圆(x-2)2+(y-1)2=9有2条公切线.分析 分别求出两圆的半径和圆心距,由此得到两圆相交,从而能求出两公切线的条数.
解答 解:∵圆C1:(x+2)2+y2=4的圆心C1(-2,0),半径r1=2,
圆C2:(x-2)2+(y-1)2=9的圆心C2(2,1),半径r2=3,
|C1C2|=$\sqrt{17}$,
∵|r1-r2|<|C1C2|<r1+r2,
∴圆C1:(x+2)2+y2=4与圆C2:(x-2)2+(y-1)2=9相交,
∴公切线有2条.
故答案为:2.
点评 本题考查两圆的公切线的条数的求法,是基础题,解题时要注意两圆位置关系的合理运用.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
5.过平面外一点,可以作这个平面的平行线的条数是( )
| A. | 1条 | B. | 2条 | C. | 超过2条但有限 | D. | 无数条 |
6.已知${(1-x)^5}={a_0}+{a_1}x+{a_2}{x^2}+{a_3}{x^3}+{a_4}{x^4}+{a_5}{x^5}$,则(a0+a2+a4)(a1+a3+a5)的值等于( )
| A. | 16 | B. | -32 | C. | 256 | D. | -256 |
3.设全集$U=\left\{{({x,y})\left|{y=x+1,x,y∈R}\right.}\right\},M=\left\{{({x,y})\left|{\frac{y-3}{x-2}=1}\right.}\right\}$,则∁UM=( )
| A. | ∅ | B. | {(2,3)} | C. | (2,3) | D. | {2,3} |
4.f(x)是偶函数且在[0,+∞)上是减函数,且f(log2x)>f(1),则x的取值范围是( )
| A. | ($\frac{1}{2}$,1) | B. | (0,$\frac{1}{2}$)∪(1,+∞) | C. | ($\frac{1}{2}$,2) | D. | (0,1)∪(2,+∞) |
5.已知i是虚数单位,则复数($\frac{1+i}{1-i}$)5的值为( )
| A. | i | B. | -i | C. | 1 | D. | -1 |
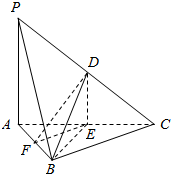 如图所示,在三棱锥P-ABC中,D,E,F分别为棱PC,AC,AB的中点.已知PA⊥AC,PA=6,BC=8,DF=5.
如图所示,在三棱锥P-ABC中,D,E,F分别为棱PC,AC,AB的中点.已知PA⊥AC,PA=6,BC=8,DF=5.