题目内容
5.已知$\overrightarrow{a}$=(2,-1),$\overrightarrow{b}$=(3,-2),则($\overrightarrow{a}$+$\overrightarrow{b}$)•($\overrightarrow{a}$-$\overrightarrow{b}$)=-8.分析 利用向量模的计算公式及其运算性质即可得出.
解答 解:∵$\overrightarrow{a}$=(2,-1),$\overrightarrow{b}$=(3,-2),
$|\overrightarrow{a}|$2=5,$|\overrightarrow{b}|$2=13.
则($\overrightarrow{a}$+$\overrightarrow{b}$)•($\overrightarrow{a}$-$\overrightarrow{b}$)=${\overrightarrow{a}}^{2}-{\overrightarrow{b}}^{2}$=5-13=-8.
故答案为:-8.
点评 本题考查了向量模的计算公式及其运算性质,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
15.曲线y=4-x3在点(-1,5)处的切线方程是( )
| A. | 3x+y-2=0 | B. | y=7x+2 | C. | y=x-4 | D. | y=7x+4 |
16.G为△ADE的重心,点P为△DEG内部(含边界)上任一点,B,C均为AD,AE上的三等分点(靠近点A),$\overrightarrow{AP}$=α$\overrightarrow{AB}$+β$\overrightarrow{AC}$(α,β∈R),则α+$\frac{1}{2}$β的范围是( )
| A. | [1,2] | B. | [1,$\frac{3}{2}$] | C. | [$\frac{3}{2}$,2] | D. | [$\frac{3}{2}$,3] |
10.设U=R,M={x|x2-2x>0},则∁RM=( )
| A. | [0,2] | B. | (0,2) | C. | (-∞,0)∪(2,+∞) | D. | (-∞,0]∪[2,+∞) |
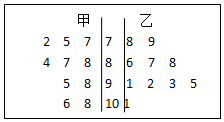 在某次考试中,从甲、乙两个班各抽取10名学生的数学成绩进行统计分析,两个班成绩的茎叶图如图所示.
在某次考试中,从甲、乙两个班各抽取10名学生的数学成绩进行统计分析,两个班成绩的茎叶图如图所示.