题目内容
15.求函数y=2sin(2x+$\frac{π}{3}$)x∈[0,π]的单调递增区间.分析 根据正弦函数的单调性求出函数的增区间D,然后与[0,π]取交集即可.
解答 解:令-$\frac{π}{2}$+2kπ≤2x+$\frac{π}{3}$≤$\frac{π}{2}$+2kπ,解得-$\frac{5π}{12}$+kπ≤x≤$\frac{π}{12}$+kπ.
[-$\frac{5π}{12}$+kπ,$\frac{π}{12}$+kπ]∩[0,π]=[0,$\frac{π}{12}$]∪[$\frac{7π}{12}$,π].
∴函数的单调递增区间为[0,$\frac{π}{12}$],[$\frac{7π}{12}$,π].
点评 本题考查了正弦函数的图象与性质,属于基础题.

练习册系列答案
相关题目
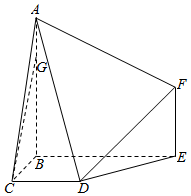 如图,多面体ABCDEF中,BA,BC,BE两两垂直,且AB∥EF,CD∥BE,AB=BE=2,BC=CD=EF=1.
如图,多面体ABCDEF中,BA,BC,BE两两垂直,且AB∥EF,CD∥BE,AB=BE=2,BC=CD=EF=1.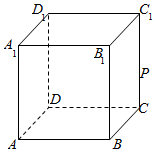 如图,在棱长为1的正方体ABCD-A1B1C1D1中,P是侧棱CC1上的一点,CP=m.
如图,在棱长为1的正方体ABCD-A1B1C1D1中,P是侧棱CC1上的一点,CP=m.