题目内容
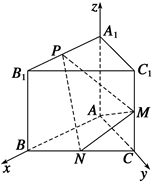
如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直, AA1=AB=AC=1,AB⊥AC, M是CC1的中点, N是BC的中点,点P在线段A1B1上,且满足A1P=lA1B1.
(1)证明:PN⊥AM.
(2)当λ取何值时,直线PN与平面ABC所成的角θ最大?并求该角最大值的正切值.
(3)是否存在点P,使得平面 PMN与平面ABC所成的二面角为45°.若存在求出l的值,若不存在,说明理由.
(1)证明:PN⊥AM.
(2)当λ取何值时,直线PN与平面ABC所成的角θ最大?并求该角最大值的正切值.
(3)是否存在点P,使得平面 PMN与平面ABC所成的二面角为45°.若存在求出l的值,若不存在,说明理由.

(1)见解析;(2)(tan θ)max=2;(3)不存在.
第一问中利用以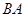 为
为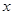 轴,
轴,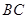 为
为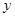 轴,
轴,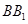 为
为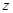 轴建立空间直角坐标系
轴建立空间直角坐标系
设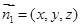 为平面
为平面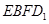 的法向量,又正方体的棱长为1,
的法向量,又正方体的棱长为1,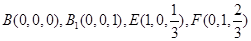
借助于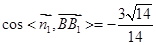 ,得到结论
,得到结论
第二问中,平面ABC的一个法向量为n=(0,0,1),
则sin θ=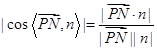 =
=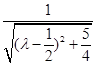 (*)
(*)
而θ∈[0,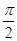 ],当θ最大时,sin θ最大,tan θ最大(θ=
],当θ最大时,sin θ最大,tan θ最大(θ=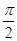 除外),
除外),
由(*)式,当λ= 时,(sin θ)max=
时,(sin θ)max=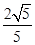 ,(tan θ)max=2
,(tan θ)max=2
第三问中,平面ABC的一个法向量为n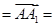 (0,0,1).设平面PMN的一个法向量为m=(x,y,z),
(0,0,1).设平面PMN的一个法向量为m=(x,y,z),
由(1)得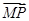 =(λ,-1,
=(λ,-1, ).
).
由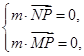 求出法向量,然后结合二面角得到解得λ=-
求出法向量,然后结合二面角得到解得λ=- .
.
(1)证明 如图,以AB,AC,AA1分别为x,y,z轴,建立空间直角坐标系A-xyz.则P(λ,0,1),N( ,
, ,0),
,0),
从而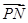 =(
=( -λ,
-λ,  ,-1),
,-1),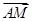 =(0,1,
=(0,1,  ).
).
\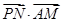 =(
=( -λ)×0+
-λ)×0+ ×1-1×
×1-1× =0,
=0,
∴PN⊥AM. -------------4分
(2)解 平面ABC的一个法向量为n=(0,0,1),
则sin θ=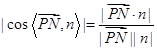 =
=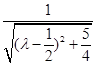 (*)
(*)
而θ∈[0,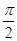 ],当θ最大时,sin θ最大,tan θ最大(θ=
],当θ最大时,sin θ最大,tan θ最大(θ=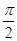 除外),
除外),
由(*)式,当λ= 时,(sin θ)max=
时,(sin θ)max=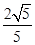 ,(tan θ)max=2 -----------6分
,(tan θ)max=2 -----------6分
(3)平面ABC的一个法向量为n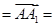 (0,0,1).设平面PMN的一个法向量为m=(x,y,z),
(0,0,1).设平面PMN的一个法向量为m=(x,y,z),
由(1)得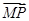 =(λ,-1,
=(λ,-1, ).
).
由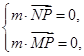
令x=3,得m=(3,2λ+1,2(1-λ)).
∵平面PMN与平面ABC所成的二面角为45°,
∴|cos〈m,n〉|=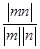 =
=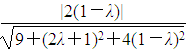 =
=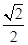 ,解得λ=-
,解得λ=- .
.
故在线段A1B1上不存在点P --------------6分
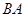 为
为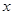 轴,
轴,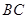 为
为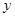 轴,
轴,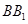 为
为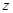 轴建立空间直角坐标系
轴建立空间直角坐标系设
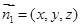 为平面
为平面 的法向量,又正方体的棱长为1,
的法向量,又正方体的棱长为1,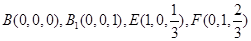
借助于
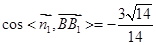 ,得到结论
,得到结论第二问中,平面ABC的一个法向量为n=(0,0,1),
则sin θ=
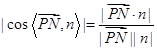 =
=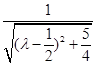 (*)
(*)而θ∈[0,
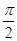 ],当θ最大时,sin θ最大,tan θ最大(θ=
],当θ最大时,sin θ最大,tan θ最大(θ=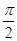 除外),
除外),由(*)式,当λ=
 时,(sin θ)max=
时,(sin θ)max=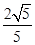 ,(tan θ)max=2
,(tan θ)max=2 第三问中,平面ABC的一个法向量为n
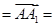 (0,0,1).设平面PMN的一个法向量为m=(x,y,z),
(0,0,1).设平面PMN的一个法向量为m=(x,y,z),由(1)得
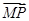 =(λ,-1,
=(λ,-1, ).
).由
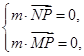 求出法向量,然后结合二面角得到解得λ=-
求出法向量,然后结合二面角得到解得λ=- .
.(1)证明 如图,以AB,AC,AA1分别为x,y,z轴,建立空间直角坐标系A-xyz.则P(λ,0,1),N(
 ,
, ,0),
,0),从而
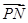 =(
=( -λ,
-λ,  ,-1),
,-1),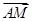 =(0,1,
=(0,1,  ).
).\
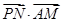 =(
=( -λ)×0+
-λ)×0+ ×1-1×
×1-1× =0,
=0, 
∴PN⊥AM. -------------4分
(2)解 平面ABC的一个法向量为n=(0,0,1),
则sin θ=
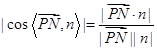 =
=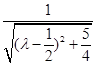 (*)
(*)而θ∈[0,
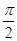 ],当θ最大时,sin θ最大,tan θ最大(θ=
],当θ最大时,sin θ最大,tan θ最大(θ=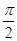 除外),
除外),由(*)式,当λ=
 时,(sin θ)max=
时,(sin θ)max=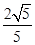 ,(tan θ)max=2 -----------6分
,(tan θ)max=2 -----------6分(3)平面ABC的一个法向量为n
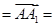 (0,0,1).设平面PMN的一个法向量为m=(x,y,z),
(0,0,1).设平面PMN的一个法向量为m=(x,y,z),由(1)得
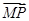 =(λ,-1,
=(λ,-1, ).
).由
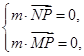
令x=3,得m=(3,2λ+1,2(1-λ)).
∵平面PMN与平面ABC所成的二面角为45°,
∴|cos〈m,n〉|=
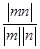 =
=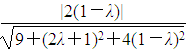 =
=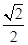 ,解得λ=-
,解得λ=- .
.故在线段A1B1上不存在点P --------------6分

练习册系列答案
相关题目
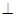 底面ABCD,
底面ABCD,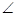 DAB为直角,AB‖CD,AD=CD=2AB,E、F分别为PC、CD的中点.
DAB为直角,AB‖CD,AD=CD=2AB,E、F分别为PC、CD的中点.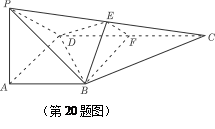
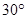 ,求k的取值范围.
,求k的取值范围. 为正方形,
为正方形,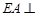 平面
平面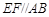 ,
,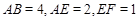 .
.
 在线段
在线段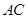 上,且满足
上,且满足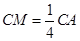 ,求证:
,求证: 平面
平面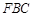 ;
;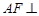 平面
平面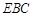 ;
; 的余弦值.
的余弦值.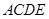 所在的平面垂直于平面
所在的平面垂直于平面 ,
, ,
, ,
, .
. 上是否存在一点
上是否存在一点 ,使得
,使得 平面
平面 ?请证明你的结论;
?请证明你的结论;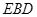 与平面
与平面 的余弦值。
的余弦值。
 中,底面
中,底面 是矩形,已知
是矩形,已知 ,
, ,
, ,
, ,
, 。
。 平面
平面 ;
; 的正切值的大小。(12分)
的正切值的大小。(12分)
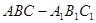 中,
中, ⊥面
⊥面 ,
,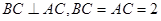 ,
, ,
,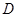 为
为 的中点.
的中点. ;
;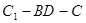 的余弦值;
的余弦值;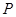 ,使得
,使得 ?请证明你的结论.
?请证明你的结论.

 ,直线
,直线 ,则下列四个命题:①
,则下列四个命题:①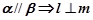 ;②
;② ;③
;③ ;④
;④ .其中正确的是( ).
.其中正确的是( ).  ,
, 是两个不同的平面,m ,n 是两条不同的直线,则下列正确的是
是两个不同的平面,m ,n 是两条不同的直线,则下列正确的是
