题目内容
若A,B,C是锐角三角形ABC的三个内角,向量 ,
, ,则
,则 与
与 的夹角为
的夹角为
- A.锐角
- B.直角
- C.钝角
- D.以上都不对
A
分析:利用两个向量数量积公式求得 =-cos(A+B),再由
=-cos(A+B),再由  =
= cos<
cos< >0,可得cos<
>0,可得cos< >>0,可得
>>0,可得  与
与 的夹角为锐角.
的夹角为锐角.
解答:∵A,B,C是锐角三角形ABC的三个内角,向量 ,
, ,
,
∴ =(cosA,sinA)•(-cosB,sinB)=-coaAcosB+sinAsinB=-(coaAcosB-sinAsinB )=-cos(A+B).
=(cosA,sinA)•(-cosB,sinB)=-coaAcosB+sinAsinB=-(coaAcosB-sinAsinB )=-cos(A+B).
由 π>A+B> ,可得 cos(A+B)<0,-cos(A+B)>0.
,可得 cos(A+B)<0,-cos(A+B)>0.
再由 =
= cos<
cos< >0,可得cos<
>0,可得cos< >>0,
>>0,
故 与
与 的夹角为锐角,
的夹角为锐角,
故选A.
点评:本题主要考查两个向量的数量积的定义,两个向量数量积公式的应用,以及三角函数在各个象限中的符号,属于中档题.
分析:利用两个向量数量积公式求得
 =-cos(A+B),再由
=-cos(A+B),再由  =
= cos<
cos< >0,可得cos<
>0,可得cos< >>0,可得
>>0,可得  与
与 的夹角为锐角.
的夹角为锐角.解答:∵A,B,C是锐角三角形ABC的三个内角,向量
 ,
, ,
,∴
 =(cosA,sinA)•(-cosB,sinB)=-coaAcosB+sinAsinB=-(coaAcosB-sinAsinB )=-cos(A+B).
=(cosA,sinA)•(-cosB,sinB)=-coaAcosB+sinAsinB=-(coaAcosB-sinAsinB )=-cos(A+B).由 π>A+B>
 ,可得 cos(A+B)<0,-cos(A+B)>0.
,可得 cos(A+B)<0,-cos(A+B)>0.再由
 =
= cos<
cos< >0,可得cos<
>0,可得cos< >>0,
>>0,故
 与
与 的夹角为锐角,
的夹角为锐角,故选A.
点评:本题主要考查两个向量的数量积的定义,两个向量数量积公式的应用,以及三角函数在各个象限中的符号,属于中档题.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
若A、B、C是锐角△ABC的三个内角,向量
=(1+sinA,1+cosA),
=(1+sinB,-1-cosB),则
与
的夹角是( )
| P |
| q |
| p |
| q |
| A、锐角 | B、钝角 | C、直角 | D、不确定 |
 ,
,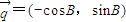 ,若A,B,C是锐角△ABC的三个内角,,则
,若A,B,C是锐角△ABC的三个内角,,则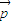 与
与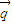 的夹角为( )
的夹角为( )