题目内容
12.已知向量$\overrightarrow{OA}$=(2,-2),$\overrightarrow{OB}$=(4,1),P点在x轴上.(1)使$\overrightarrow{AP}$•$\overrightarrow{BP}$最小,求P坐标;
(2)若∠APB为钝角,求P横坐标的取值范围.
分析 (1)设P(x,0),可得$\overrightarrow{AB}$、$\overrightarrow{BP}$含有x的坐标形式,由向量数量积的坐标运算公式得$\overrightarrow{AP}$•$\overrightarrow{BP}$=x2-6x+10,结合二次函数的图象与性质,可得当x=3时$\overrightarrow{AP}$•$\overrightarrow{BP}$取得最小值1,得到本题答案;
(2)若∠APB为钝角,即有$\overrightarrow{PA}$•$\overrightarrow{PB}$<0,且有$\overrightarrow{PA}$,$\overrightarrow{PB}$不共线.设P(m,0),求得向量PA,PB的坐标,由向量的数量积的坐标表示和向量共线的坐标表示,解不等式即可得到所求范围.
解答 解:(1)设点P的坐标为(x,0),
可得$\overrightarrow{AP}$=(x-2,2),$\overrightarrow{BP}$=(x-4,-1).
因此$\overrightarrow{AP}$•$\overrightarrow{BP}$=(x-4)(x-2)-2=x2-6x+6=(x-3)2-3.
∵二次函数y=(x-3)2-3,当x=3时取得最小值为-3.
∴当x=3时,$\overrightarrow{AP}$•$\overrightarrow{BP}$取得最小值-3,此时P(3,0);
(2)若∠APB为钝角,即有$\overrightarrow{PA}$•$\overrightarrow{PB}$<0,且有$\overrightarrow{PA}$,$\overrightarrow{PB}$不共线.
设P(m,0),即有$\overrightarrow{PA}$=(2-m,-2),$\overrightarrow{PB}$=(4-m,1),
则(2-m)(4-m)<0,解得2<m<4.
由$\overrightarrow{PA}$,$\overrightarrow{PB}$共线,可得2-m=-2(4-m),解得m=$\frac{10}{3}$
则有P的横坐标的范围是(2,$\frac{10}{3}$)∪($\frac{10}{3}$,4).
点评 本题给出向量$\overrightarrow{OA}$,$\overrightarrow{OB}$的坐标,求在x轴上一点P,使$\overrightarrow{AP}$•$\overrightarrow{BP}$有最小值以及∠APB为钝角,着重考查了向量数量积的坐标运算公式和二次函数的性质等知识,同时考查向量的夹角为钝角的条件,属于中档题.

 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案| A. | 2x+2y+1=0 | B. | 2x+2y-1=0 | C. | 2x-2y-1=0 | D. | 2x-2y-3=0 |
| A. | $\frac{17\sqrt{17}}{6}π$ | B. | 17π | C. | $\frac{17π}{2}$ | D. | $\frac{17π}{4}$ |
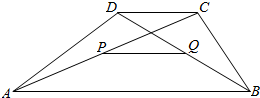 设P,Q分别是梯形ABCD的对角线AC与BD的中点
设P,Q分别是梯形ABCD的对角线AC与BD的中点 .
. 在点
在点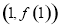 处的切线方程为
处的切线方程为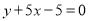 ,求函数
,求函数 是函数
是函数 ,求
,求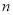 的值;
的值; 时,函数
时,函数 ,且
,且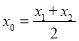 ,求证:
,求证: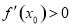 .
.