题目内容
抛物线x2=2py（p＞0）过焦点F的直线l交抛物线于A、B两点，O为原点，若△AOB面积最小值为8．
（1）求P值
（2）过A点作抛物线的切线交y轴于N，
=
+
，则点M在一定直线上，试证明之．
（1）求P值
（2）过A点作抛物线的切线交y轴于N，
| FM |
| FA |
| FN |
考点：抛物线的简单性质
专题：圆锥曲线的定义、性质与方程
分析：（1）抛物线x2=2py的焦点F(0，
)，设直线l方程为y=kx+
，与抛物线方程联立可得x2-2pkx-p2=0，设A（x1，y1），B（x2，y2），S△AOB=S△AOF+S△BOF=
|OF|•|x1-x2|=
≥
，即可得出．
（2）由x2=8y，利用导数可得y′=
，过A点的切线方程为y=
(x-x1)+
，可得N（0，-y1），设M（x，y），又F（0，2），利用
=
+
，可得
，即可证明．
| p |
| 2 |
| p |
| 2 |
| 1 |
| 2 |
| p2 |
| 2 |
| k2+1 |
| p2 |
| 2 |
（2）由x2=8y，利用导数可得y′=
| x |
| 4 |
| x1 |
| 4 |
| ||
| 8 |
| FM |
| FA |
| FN |
|
解答：
（1）解：∵抛物线x2=2py的焦点F(0，
)，
∴设直线l方程为y=kx+
，
由
，消去y得x2-2pkx-p2=0，
设A（x1，y1），B（x2，y2），
S△AOB=S△AOF+S△BOF=
|OF|•|x1|+
|OF|•|x2|=
|OF|•|x1-x2|
=
•
=
≥
，当k=0的等号成立，
∴S△AOB面积的最小值为
，
∴
=8，
∵p＞0，∴p=4．
（2）证明：∵x2=8y，∴y′=
，
∴过A点的切线方程为y=
(x-x1)+
，
即y=
x1x-
=
x1x-y1，
∴N（0，-y1），
设M（x，y），
又∵F（0，2），
∴
=（x，y-2），
=（x1，y1-2），
=（0，-y1-2），
∵
=
+
，
∴
，
得
，
∴M点在直线y=-2上．
| p |
| 2 |
∴设直线l方程为y=kx+
| p |
| 2 |
由
|
设A（x1，y1），B（x2，y2），
S△AOB=S△AOF+S△BOF=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| P |
| 4 |
| 4p2k2+4p2 |
| p2 |
| 2 |
| k2+1 |
| p2 |
| 2 |
∴S△AOB面积的最小值为
| p2 |
| 2 |
∴
| p2 |
| 2 |
∵p＞0，∴p=4．
（2）证明：∵x2=8y，∴y′=
| x |
| 4 |
∴过A点的切线方程为y=
| x1 |
| 4 |
| ||
| 8 |
即y=
| 1 |
| 4 |
| 1 |
| 8 |
| x | 2 1 |
| 1 |
| 4 |
∴N（0，-y1），
设M（x，y），
又∵F（0，2），
∴
| FM |
| FA |
| FN |
∵
| FM |
| FA |
| FN |
∴
|
得
|
∴M点在直线y=-2上．
点评：本题考查了直线与抛物线相交相切问题、弦长公式、三角形的面积计算公式、向量坐标运算、切线方程、二次函数的单调性，考查了推理能力与计算能力，属于难题．
练习册系列答案
相关题目
已知数列{an}的递推公式an=
，则a2012+a2013=（ ）
|
| A、2516 | B、2518 |
| C、3019 | D、3021 |
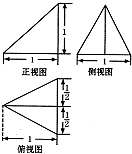
已知某几何体的三视图，根据图中标出的尺寸，可得这个几何体的体积是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|