题目内容
已知|a|=2|b|≠0,且关于x的函数f(x)=
x3+
|a|x2+a·bx在R上有极值,则向量a与b的夹角的范围是( )
(A)[0,
) (B)(,π]
(C)(
,π] (D)(,
π)
C解析:设a与b的夹角为θ.
∵f(x)=x3+|a|x2+a·bx,
∴f′(x)=x2+|a|x+a·b.
∵函数f(x)在R上有极值,
∴方程x2+|a|x+a·b=0有两个不同的实数根,
即Δ=|a|2-4a·b>0,∴a·b<
,
又∵|a|=2|b|≠0,∴cos θ=
<
=,
即cos θ<,又∵θ∈[0,π],∴θ∈(,π],故选C.
练习册系列答案
相关题目
,cos β=
),则α+β= .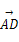 
=(3,7),
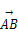=(-2,3),对角线AC与BD交于点O,则
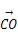的坐标为( )
,5) (B)(
(C)1 (D)
＝
，M，N分别为AD，BC的中点．设
＝
，
，试用
表示
，
.
＝16，|
＋
|＝|
|＝ ( )．
，
是两个不共线的向量，则向量
＝－
＝
－2
中，
，
，则
.