题目内容
9.已知函数f(x)=ex-ax-1(a为常数)在x=ln2处取得极值.(1)求实数a的值及函数f(x)的单调区间;
(2)证明:当x>0时,ex>x2+1.
分析 (1)求出函数的f′(x)=ex-a.通过f′(x)=ex-2>0,即可求解函数f(x)在区间(-∞,ln2)上单调递减,在(ln2,+∞)上单调递增.
(2)求出f(x)的最小值,化简f(x)≥1-ln4.构造g(x)=ex-x2-1,通过g′(x)>0.判断g(x)在(0,+∞)上单调递增,得到g(x)>g(0),推出结果.
解答 解:(1)由f(x)=ex-ax-1,得f′(x)=ex-a.
又f′(ln2)=2-a=-0,所以a=2,
所以f(x)=ex-2x-1,f′(x)=ex-2.
由f′(x)=ex-2>0,得x>ln2.
所以函数f(x)在区间(-∞,ln2)上单调递减,在(ln2,+∞)上单调递增.…(4分)
(2)证明:由(1)知f(x)min=f(ln2)=eln2-2ln2-1=1-ln4.
所以f(x)≥1-ln4,即ex-2x-1≥1-ln4,ex-2x≥2-ln4>0.
令g(x)=ex-x2-1,则g'(x)=ex-2x>0.
所以g(x)在(0,+∞)上单调递增,所以g(x)=ex-x2-1>g(0)=0,即ex>x2+1.…(8分)
点评 本题考查函数的导数的应用,函数的导数的最值的应用,考查分析问题解决问题的能力,属于中档题.

练习册系列答案
相关题目
18.若tan α<0,则( )
| A. | sin α<0 | B. | cos α<0 | C. | sin α•cosα<0 | D. | sin α-cos α<0 |
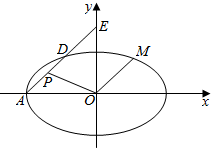 如图,在平面直角坐标系xoy中,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率e=$\frac{1}{2}$,左顶点为A(-4,0),过点A作斜率为k(k≠0)的直线l交椭圆C于点D,交y轴于点E.
如图,在平面直角坐标系xoy中,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率e=$\frac{1}{2}$,左顶点为A(-4,0),过点A作斜率为k(k≠0)的直线l交椭圆C于点D,交y轴于点E. 如图所示,O为坐标原点,过点P(4,0)且斜率为k的直线l交抛物线y2=4x于M(x1,y1),N(x2,y2)两点.
如图所示,O为坐标原点,过点P(4,0)且斜率为k的直线l交抛物线y2=4x于M(x1,y1),N(x2,y2)两点.