题目内容
设命题p:“对任意的x∈R,x2+2x>m”,
命题q:“存在x∈R,使x2-2mx+3-2m=0”.
如果命题p∨q为真,命题p∧q为假,求实数m的取值范围.
命题q:“存在x∈R,使x2-2mx+3-2m=0”.
如果命题p∨q为真,命题p∧q为假,求实数m的取值范围.
考点:复合命题的真假
专题:简易逻辑
分析:首先求出命题p所符合的解集,进一步求出命题q的解集,利用且是命题和或是命题进一步求出结果.
解答:
解:命题p:“对任意的x∈R,x2+2x>m”,
只需满足(x2+2x)min>m即可.
所以:设f(x)=x2+2x=(x+1)2-1,
由于x∈R,所以f(x)min=-1,
即m<-1;
命题q:“存在x∈R,使x2-2mx+3-2m=0”.
只需满足x2-2mx+3-2m=0有解即可,
所以:△=4m2-4(3-2m)≥0,
解得:m≥1或m≤-3.
命题p∨q为真,命题p∧q为假,
所以:①p真q假,
则:
,
解得:-3<m<-1;
②p假q真,
则:
解得:m≥1;
综上所述:m的取值范围为:m≥1或-3<m<-1.
只需满足(x2+2x)min>m即可.
所以:设f(x)=x2+2x=(x+1)2-1,
由于x∈R,所以f(x)min=-1,
即m<-1;
命题q:“存在x∈R,使x2-2mx+3-2m=0”.
只需满足x2-2mx+3-2m=0有解即可,
所以:△=4m2-4(3-2m)≥0,
解得:m≥1或m≤-3.
命题p∨q为真,命题p∧q为假,
所以:①p真q假,
则:
|
解得:-3<m<-1;
②p假q真,
则:
|
解得:m≥1;
综上所述:m的取值范围为:m≥1或-3<m<-1.
点评:本题考查的知识要点:复合命题的应用,且是命题和或是命题的应用,不等式组的应用,属于基础题型.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
设定点F1(0,-3)、F2(0,3)动点P满足条件|PF1|-a=
-|PF2|(a>0)则点P的轨迹是( )
| 9 |
| a |
| A、椭圆 | B、线段 |
| C、不存在 | D、椭圆或线段 |
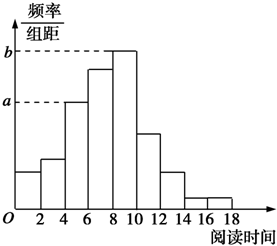 从某校随机抽取100名学生,获得了他们一周课外阅读时间(单位:小时)的数据,整理得到数据分组及频率分布表和频率分布直方图:
从某校随机抽取100名学生,获得了他们一周课外阅读时间(单位:小时)的数据,整理得到数据分组及频率分布表和频率分布直方图: