题目内容
函数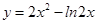 的的单调递增区间是 ( )
的的单调递增区间是 ( )
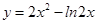 的的单调递增区间是 ( )
的的单调递增区间是 ( )A. | B.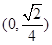 |
C.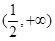 | D.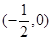 和 和 |
C
试题分析:求出f(x)的导函数,令导函数大于0列出关于x的不等式,求出不等式的解集即可得到x的范围即为函数的单调递增区间.对于函数
 ,可知当y’>0,可知得到
,可知当y’>0,可知得到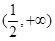 函数递增,故答案为C.
函数递增,故答案为C.点评:本题主要考查学生会利用导函数的正负得到函数的单调区间,同时考查了导数的计算,是一道基础题.

练习册系列答案
相关题目
题目内容
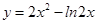 的的单调递增区间是 ( )
的的单调递增区间是 ( )A. | B.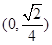 |
C.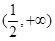 | D.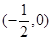 和 和 |
 ,可知当y’>0,可知得到
,可知当y’>0,可知得到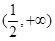 函数递增,故答案为C.
函数递增,故答案为C.