Question

已知椭圆:的焦距为,离心率为,其右焦点为,过点作直线交椭圆于另一点．

（1）若,求外接圆的方程;

（2）若过点的直线与椭圆相交于两点、，设为上一点，且满足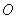（为坐标原点），当时，求实数的取值范围．

Answer 1

解：（1）由题意知：，，又，

解得：椭圆的方程为：               2分

可得：，,设，则，，

，，即

由，或

即，或                        4分

①当的坐标为时，，外接圆是以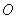为圆心，为半径的圆，即                       5分

②当的坐标为时，，，所以为直角三角形，其外接圆是以线段为直径的圆，圆心坐标为，半径为，

外接圆的方程为

综上可知：外接圆方程是，或   6分

（2）由题意可知直线的斜率存在．

设，，，

由得：

由得：（）               8分

，即

，结合（）得：                     10分

，

从而，

点在椭圆上，，整理得：

即，，或            12分