题目内容
12.设函数$f(x)=\frac{{{{(sinx+1)}^2}}}{{{{sin}^2}x+1}}$的最大值为M,最小值为m,则M+m=2.分析 通过换元可知y=f(x)=1+$\frac{2t}{{t}^{2}+1}$,其中t=sinx∈[-1,1],利用z=$\frac{2t}{{t}^{2}+1}$为奇函数可知zmax+zmin=0,进而M+m=(1+zmax)+(1+zmin)=2.
解答 解:由题可知t=sinx∈[-1,1],则y=f(x)=1+$\frac{2t}{{t}^{2}+1}$,
令z=$\frac{2t}{{t}^{2}+1}$,则当t=0时z=0,且函数z为奇函数,
所以zmax+zmin=0,
又因为M+m=(1+zmax)+(1+zmin),
所以M+m=2+(zmax+zmin)=2,
故答案为:2.
点评 本题考查函数的最值及其几何意义,考查函数的奇偶性,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
7.已知$sinα=\frac{{\sqrt{10}}}{10}$,$sin(α-β)=-\frac{{\sqrt{5}}}{5}$,$α,β∈(0,\frac{π}{2})$,则β=( )
| A. | $\frac{5π}{12}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |
1.已知i是虚数单位,复数z满足z=i(i-1),则z的虚部是( )
| A. | 1 | B. | -1 | C. | i | D. | -i |
2.如图,△A'B'C'是△ABC的直观图,其中A'B'=A'C',那么△ABC是( )
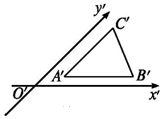

| A. | 等腰三角形 | B. | 直角三角形 | C. | 等腰直角三角形 | D. | 钝角三角形 |
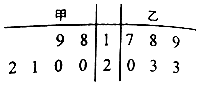 甲、乙两名技工在相同的条件下生产某种零件,连续6天中,他们日加工的合格零件数的统计数据的茎叶图,如图所示.
甲、乙两名技工在相同的条件下生产某种零件,连续6天中,他们日加工的合格零件数的统计数据的茎叶图,如图所示.