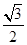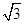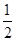题目内容
已知抛物线和椭圆都经过点
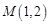 ,它们在
,它们在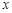 轴上有共同焦点,椭圆的对称轴是坐标轴,抛物线的顶点为坐标原点.
轴上有共同焦点,椭圆的对称轴是坐标轴,抛物线的顶点为坐标原点.(1)求这两条曲线的方程;
(2)对于抛物线上任意一点
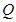 ,点
,点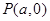 都满足
都满足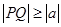 ,求
,求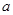 的取值范围.
的取值范围.(1)  ,
,
(2)
 ,
,
(2)

试题分析:解:(1)设抛物线方程为
 ,将
,将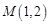 代入方程得
代入方程得
 -------------------2分
-------------------2分由题意知椭圆、双曲线的焦点为
 3分
3分对于椭圆,

 ,
, 
所以椭圆方程为
 - -6分
- -6分(2)设
 ------------(7分)
------------(7分)由
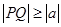 得
得 - (9分)
- (9分) 恒成立 10分
恒成立 10分则

∴
 12分
12分点评:解决的关键是根据圆锥曲线的性质来求解其方程,同时在抛物线中利用两点的距离公式结合不等式来得到求解范围,注意中档题。

练习册系列答案
相关题目
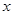 轴上的双曲线
轴上的双曲线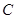 的离心率为
的离心率为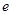 ,直线与双曲线
,直线与双曲线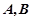 两点,线段
两点,线段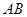 中点
中点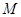 在第一象限,并且在抛物线
在第一象限,并且在抛物线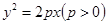 上,且
上,且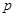 ,则直线的斜率为( )
,则直线的斜率为( )
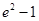
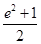
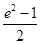
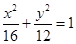 上找一点,使这一点到直线
上找一点,使这一点到直线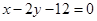 的距离的最小值
的距离的最小值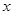 轴上的椭圆
轴上的椭圆 的离心率为
的离心率为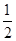 ,则
,则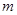 的值为( )
的值为( )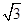
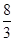
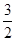
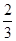
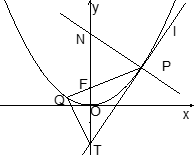
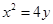 的焦点
的焦点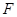 作倾斜角为
作倾斜角为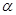 的直线交抛物线于
的直线交抛物线于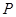 、
、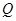 两点,过点
两点,过点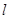 交
交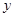 轴于点
轴于点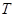 ,过点
,过点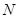 。
。
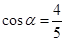 ,求此抛物线与线段
,求此抛物线与线段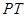 以及线段
以及线段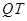 所围成的封闭图形的面积。
所围成的封闭图形的面积。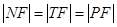 ;
;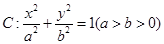 的离心率为
的离心率为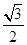 .双曲线
.双曲线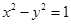 的渐近线与椭圆
的渐近线与椭圆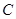 有四个交点,以这四个交点为顶点的四边形的面积为16,则椭圆
有四个交点,以这四个交点为顶点的四边形的面积为16,则椭圆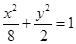


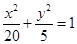
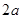 ,焦点是
,焦点是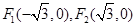 ,点
,点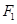 到直线
到直线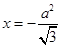 的距离为
的距离为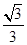 ,过点
,过点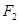 且倾斜角为锐角的直线
且倾斜角为锐角的直线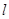 与椭圆交于A、B两点,使得|
与椭圆交于A、B两点,使得|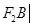 =3|
=3|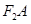
 .
.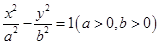 的左焦点
的左焦点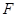 引圆
引圆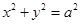 的切线,切点为
的切线,切点为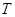 ,延长
,延长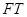 交双曲线右支于
交双曲线右支于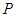 点,若
点,若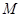 为线段
为线段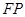 的中点,
的中点,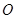 为坐标原点,则
为坐标原点,则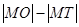 与
与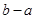 的大小关系为( )
的大小关系为( )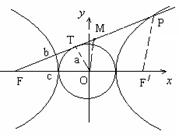
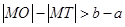
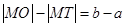
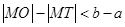
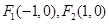 为椭圆
为椭圆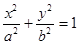 的两个焦点,若椭圆上一点
的两个焦点,若椭圆上一点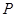 满足
满足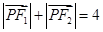 ,则椭圆的离心率
,则椭圆的离心率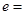 ( )
( )