题目内容
在椭圆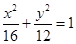 上找一点,使这一点到直线
上找一点,使这一点到直线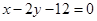 的距离的最小值
的距离的最小值
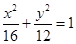 上找一点,使这一点到直线
上找一点,使这一点到直线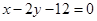 的距离的最小值
的距离的最小值
试题分析:解:设椭圆的参数方程为
 , 2分
, 2分 4分
4分 8分
8分当
 时,
时, ,此时所求点为
,此时所求点为 10分
10分点评:关键是利用椭圆的参数方程来设出点,借助于点到直线的距离公式得到最值,属于基础题。

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
题目内容
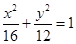 上找一点,使这一点到直线
上找一点,使这一点到直线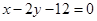 的距离的最小值
的距离的最小值
 , 2分
, 2分 4分
4分 8分
8分 时,
时, ,此时所求点为
,此时所求点为 10分
10分
 智慧小复习系列答案
智慧小复习系列答案