题目内容
函数f(x)=4x3+ax2+bx+5的图像在x=1处的切线方程为y=-12x,
(1)求函数f(x)的解析式;
(2)求函数f(x)在[-3,1]上的最值。
(1)求函数f(x)的解析式;
(2)求函数f(x)在[-3,1]上的最值。
解:(1)f′(x)=12x2+2ax+b,
∵y=f(x)在x=1处的切线方程为y=-12x,
∴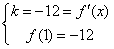 ,即
,即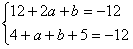 ,解得:a=-3,b=-18,
,解得:a=-3,b=-18,
∴f(x)=4x3-3x2-18x+5。
(2)∵f′(x)=12x2-6x-18=6(x+1)(2x-3),
令f′(x)=0解得:x=-1或x=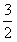 ,
,
∴当x<-1或x>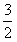 时,f′(x)>0,当-1<x<
时,f′(x)>0,当-1<x<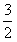 时,f′(x)<0,
时,f′(x)<0,
∵x∈[-3,1],
∴f(x)在[-3,1]上无极小值,有极大值f(-1)=16,
又∵f(-3)=-76,f(1)=-12,
∴f(x)在[-3,1]上的最小值为-76,最大值为16。
∵y=f(x)在x=1处的切线方程为y=-12x,
∴
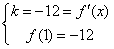 ,即
,即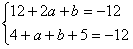 ,解得:a=-3,b=-18,
,解得:a=-3,b=-18,∴f(x)=4x3-3x2-18x+5。
(2)∵f′(x)=12x2-6x-18=6(x+1)(2x-3),
令f′(x)=0解得:x=-1或x=
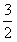 ,
, ∴当x<-1或x>
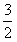 时,f′(x)>0,当-1<x<
时,f′(x)>0,当-1<x<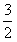 时,f′(x)<0,
时,f′(x)<0,∵x∈[-3,1],
∴f(x)在[-3,1]上无极小值,有极大值f(-1)=16,
又∵f(-3)=-76,f(1)=-12,
∴f(x)在[-3,1]上的最小值为-76,最大值为16。

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
若a>0,b>0,且函数f(x)=4x3-ax2-2bx+2在x=1处有极值,则ab的最大值等于( )
| A、2 | B、3 | C、6 | D、9 |
设函数f(x)=4x3+x-8,用二分法求方程4x3+x-8=0的近似过程中,计算得到f(1)<0,f(3)>0,则方程的根落在区间( )
| A、(1,1.5) | B、(1.5,2) | C、(2,2.5) | D、(2.5,3) |