题目内容
4.已知函数f(x)=x2+ax+sin$\frac{π}{2}$x(x∈(0,1))在定义域内单调递增,则a的取值范围是( )| A. | [-$\frac{π}{2}$,+∞) | B. | (-∞,-$\frac{π}{2}$] | C. | (-∞,0] | D. | [0,+∞) |
分析 函数f(x)在定义域内单调递增,则导函数f′(x)≥0恒成立,然后问题转化为函数的最值问题求解.
解答 解:由f(x)=x2+ax+sin$\frac{π}{2}$x,得
f′(x)=2x+a+$\frac{π}{2}•$cos$\frac{π}{2}$x,
∵函数f(x)=x2+ax+sin$\frac{π}{2}$x在(0,1)内单调递增,
∴f′(x)=2x+a+$\frac{π}{2}•$cos$\frac{π}{2}$x≥0在(0,1)内恒成立,
即a≥-2x-$\frac{π}{2}•cos\frac{π}{2}x$在(0,1)内恒成立.
令g(x)=-2x-$\frac{π}{2}•cos\frac{π}{2}x$,则g′(x)=-2+$\frac{{π}^{2}}{4}$sin$\frac{π}{2}x$,
∵g′(x)在(0,1)上递增,且g′(0)<0,g′(1)>0,
∴g′(x)在区间(0,1)上存在唯一零点m.
∴g(x)在(0,m)上递减,在(m,1)上递增.
由$\left\{\begin{array}{l}{a≥g(0)}\\{a≥g(1)}\end{array}\right.$,a$≥-\frac{π}{2}$,
∴a的取值范围是[-$\frac{π}{2}$,+∞).
故选:A.
点评 本题考查了利用导数研究函数的单调性极值与最值、通过构造函数研究函数的单调性解决问题的方法,考查了转化能力、推理能力与计算能力,属于难题.

练习册系列答案
相关题目
9.已知函数f(x)是定义在R上的奇函数,其最小正周期为3,当x∈(-$\frac{3}{2}$,0)时,f(x)=log${\;}_{\frac{1}{2}}$(1-x),则f(2011)+f(2013)=( )
| A. | 1 | B. | 2 | C. | -1 | D. | -2 |
15.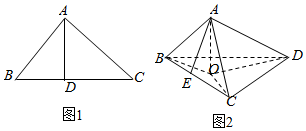 如图1所示,在△ABC中,AB⊥AC,AD⊥BC,则AB2=BD•BC.类似有命题:在三棱锥A-BCD中,如图2所示,AD⊥面ABC.若A在△BCD内的射影为O,E在BC上,且E,O,D在同一条直线上,则S△ABC2=S△BCO•S△BCD,此命题是( )
如图1所示,在△ABC中,AB⊥AC,AD⊥BC,则AB2=BD•BC.类似有命题:在三棱锥A-BCD中,如图2所示,AD⊥面ABC.若A在△BCD内的射影为O,E在BC上,且E,O,D在同一条直线上,则S△ABC2=S△BCO•S△BCD,此命题是( )
 如图1所示,在△ABC中,AB⊥AC,AD⊥BC,则AB2=BD•BC.类似有命题:在三棱锥A-BCD中,如图2所示,AD⊥面ABC.若A在△BCD内的射影为O,E在BC上,且E,O,D在同一条直线上,则S△ABC2=S△BCO•S△BCD,此命题是( )
如图1所示,在△ABC中,AB⊥AC,AD⊥BC,则AB2=BD•BC.类似有命题:在三棱锥A-BCD中,如图2所示,AD⊥面ABC.若A在△BCD内的射影为O,E在BC上,且E,O,D在同一条直线上,则S△ABC2=S△BCO•S△BCD,此命题是( )| A. | 假命题 | |
| B. | 增加AB⊥AC的条件才是真命题 | |
| C. | 真命题 | |
| D. | 增加三棱锥A-BCD是正棱锥的条件才是真命题 |
12.函数y=2sin(x-$\frac{π}{4}$)的一条对称轴是( )
| A. | x=$\frac{π}{4}$ | B. | x=$\frac{π}{2}$ | C. | x=$\frac{3π}{4}$ | D. | x=2π |
19.已知复数z满足(1-i)z=2+2i(i为虚数单位),则|z|=( )
| A. | $\sqrt{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | 2 | D. | 1 |
9.已知随机变量X的分布列为P(X=i)=$\frac{i}{3a}$(i=1,2,3,4,5),则P(1<X<4)等于( )
| A. | $\frac{1}{3}$ | B. | $\frac{3}{5}$ | C. | $\frac{5}{3a}$ | D. | $\frac{9}{3a}$ |
13.一个命题的四种形式的命题中真命题的个数可能取值是( )
| A. | 0或2 | B. | 0或4 | C. | 2或4 | D. | 0或2 或4 |
14. 执行如图所示的程序框图,输出的T的值为( )
执行如图所示的程序框图,输出的T的值为( )
 执行如图所示的程序框图,输出的T的值为( )
执行如图所示的程序框图,输出的T的值为( )| A. | 12 | B. | 17 | C. | 20 | D. | 30 |