题目内容
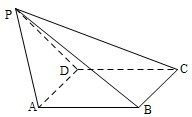 如图,已知四棱锥P-ABCD,PB⊥AD侧面PAD为边长等于2的正三角形,底面ABCD为菱形,侧面PAD与底面ABCD所成的二面角为120°.
如图,已知四棱锥P-ABCD,PB⊥AD侧面PAD为边长等于2的正三角形,底面ABCD为菱形,侧面PAD与底面ABCD所成的二面角为120°.(Ⅰ)求点P到平面ABCD的距离,
(Ⅱ)求面APB与面CPB所成二面角的余弦值.
考点:二面角的平面角及求法,点、线、面间的距离计算
专题:空间位置关系与距离,空间角
分析:(1)作PO⊥平面ABCD,垂足为点O,连结OB、OA、OD,OB与AD交于点E,连结PE,由已知得AD⊥OB,PE⊥AD,知∠PEB为面PAD与面ABCD所成二面角的平面角,从而∠PEB=120°,∠PEO=60°,由此能求出点P到平面ABCD的距离.
(2)取PB的中点G,PC的中点F,连结EG、AG、GF,由已知得∠AGF是所求二面角的平面角,由此能求出面APB与面CPB所成二面角的余弦值.
(2)取PB的中点G,PC的中点F,连结EG、AG、GF,由已知得∠AGF是所求二面角的平面角,由此能求出面APB与面CPB所成二面角的余弦值.
解答:
解:(1)作PO⊥平面ABCD,垂足为点O
连结OB、OA、OD,OB与AD交于点E,连结PE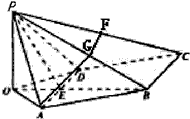
∵AD⊥PB,∴AD⊥OB,
∵PA=PD,∴OA=OD,
于是OB平分AD,点E为AD的中点,所以PE⊥AD
由此知∠PEB为面PAD与面ABCD所成二面角的平面角,
∴∠PEB=120°,∠PEO=60°
由已知可求得PE=
,
∴PO=PE•sin60°=
×
=
,
∴点P到平面ABCD的距离为
.
(2)如图,取PB的中点G,PC的中点F,连结EG、AG、GF,
则AG⊥PB,FG∥BC,FG=
BC,
∵AD⊥PB,∴BC⊥PB,FG⊥PB,
∴∠AGF是所求二面角的平面角
∵AD⊥面POB,∴AD⊥EG
又∵PE=BE,∴EG⊥PB,且∠PEG=60°
在Rt△PEG中,EG=PE•cos60°=
,
又AE=
AD=1,AG=
=
,
于是cosn∠GAE=
=
=
,
又∠AGF=π-∠GAE
∴cos∠AGF=-
.
∴面APB与面CPB所成二面角的余弦值为-
.
连结OB、OA、OD,OB与AD交于点E,连结PE

∵AD⊥PB,∴AD⊥OB,
∵PA=PD,∴OA=OD,
于是OB平分AD,点E为AD的中点,所以PE⊥AD
由此知∠PEB为面PAD与面ABCD所成二面角的平面角,
∴∠PEB=120°,∠PEO=60°
由已知可求得PE=
| 3 |
∴PO=PE•sin60°=
| 3 |
| ||
| 2 |
| 3 |
| 2 |
∴点P到平面ABCD的距离为
| 3 |
| 2 |
(2)如图,取PB的中点G,PC的中点F,连结EG、AG、GF,
则AG⊥PB,FG∥BC,FG=
| 1 |
| 2 |
∵AD⊥PB,∴BC⊥PB,FG⊥PB,
∴∠AGF是所求二面角的平面角
∵AD⊥面POB,∴AD⊥EG
又∵PE=BE,∴EG⊥PB,且∠PEG=60°
在Rt△PEG中,EG=PE•cos60°=
| ||
| 2 |
又AE=
| 1 |
| 2 |
12+(
|
| ||
| 2 |
于是cosn∠GAE=
| EG |
| AG |
| ||||
|
| ||
| 7 |
又∠AGF=π-∠GAE
∴cos∠AGF=-
| ||
| 7 |
∴面APB与面CPB所成二面角的余弦值为-
| ||
| 7 |
点评:本题考查点到平面的距离的求法,考查二面角的余弦值的求法,解题时要认真审题,涉及到线面垂直、二面角、点到平面距离、线面角等知识点,解题时要注意空间思维能力的培养.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
若函数f(x)=
在[2,+∞)上有意义,则实数a的取值范围为( )
| ax-2 |
| A、a=1 | B、a>1 |
| C、a≥1 | D、a≥0 |
执行如图所示的程序框图,若p=0.7,则输出的n为( )


| A、2 | B、3 | C、4 | D、5 |
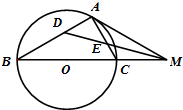 已知Rt△ABC(∠A=90°)的外接圆为圆O,过A的切线AM交BC于点M,过M作直线交AB,AC于点D,E,且AD=AE
已知Rt△ABC(∠A=90°)的外接圆为圆O,过A的切线AM交BC于点M,过M作直线交AB,AC于点D,E,且AD=AE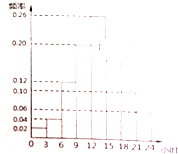 天猫电器城对TCL官方旗舰店某款4K超高清电视机在2014年11月11日的销售情况进行了统计,如图所示,数据显示,该日TCL官方旗舰店在[0,3)小时销售了该款电视机2台.
天猫电器城对TCL官方旗舰店某款4K超高清电视机在2014年11月11日的销售情况进行了统计,如图所示,数据显示,该日TCL官方旗舰店在[0,3)小时销售了该款电视机2台. 如图,已知AB⊥平面BCE,CD∥AB,△BCE是正三角形,AB=BC=2CD.
如图,已知AB⊥平面BCE,CD∥AB,△BCE是正三角形,AB=BC=2CD.