题目内容
是否存在常数 使得
使得 对一切
对一切 恒成立?若存在,求出
恒成立?若存在,求出 的值,并用数学归纳法证明;若不存在,说明理由。
的值,并用数学归纳法证明;若不存在,说明理由。
解:取 和2 得
和2 得 解得
解得 ………………………4分
………………………4分
即
以下用数学归纳法证明:
(1)当n=1时,已证。
(2)假设当n=k, 时等式成立
时等式成立
即 ………………………8分
………………………8分
那么,当 时有
时有

 ………………………12分
………………………12分
就是说,当 时等式成立
时等式成立
根据(1)(2)知,存在 使得任意
使得任意 等式都成立…………………14分
等式都成立…………………14分

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案
相关题目
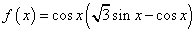 。
。 的最小正周期和单调递减区间;
的最小正周期和单调递减区间;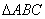 的内角
的内角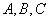 的对应边分别为
的对应边分别为 ,且
,且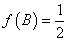 ,
,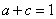 ,求
,求 的取值范围。
的取值范围。 及
及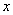 轴围成的曲边梯形的面积介于相应小矩形与大矩形的面积之间,即
轴围成的曲边梯形的面积介于相应小矩形与大矩形的面积之间,即 .类比之,
.类比之,
 ,
, 恒成立,
恒成立,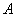 等于
等于
 B.
B.
 D.
D.
 的焦点与双曲线
的焦点与双曲线 的右焦点重合,则
的右焦点重合,则 的值为
的值为  ,则实数
,则实数 的值为
的值为  ”是真命题,则实数a的取值范围是
”是真命题,则实数a的取值范围是  的最小值为( )
的最小值为( ) C. 4 D.
C. 4 D. 
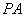 与⊙
与⊙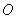 相切,
相切,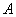 为切点,过点
为切点,过点 的割线交圆于
的割线交圆于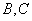 两点,弦
两点,弦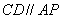 ,
, 相交于点
相交于点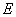 ,
,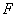 为
为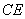 上一点,且
上一点,且 .
.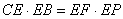 ;
;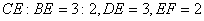 ,求
,求