��Ŀ����
16����֪����$f��x��=\left\{\begin{array}{l}-{��x-1��^2}+2��\;\;\;x��1\\ \frac{1}{x}+1��\;\;x��1\;.\;\;\end{array}\right.$�����ĸ����⣺��f��f��1������f��3����
��?x0�ʣ�1��+�ޣ���$f'��{x_0}��=-\frac{1}{3}$��
��f��x���ļ���ֵ��Ϊx=1��
��?x1��x2�ʣ�0��+�ޣ���|f��x1��-f��x2��|��1
������ȷ���Т٢ڢۢܣ���д��������ȷ�������ţ�
���� �⣺����f��x����ͼ����ͼ��ʾ��
���ڢ٣�f��1��=2��f��f��1����=f��2��=$\frac{3}{2}$��f��3��=$\frac{4}{3}$����
���ڢڣ�x��1ʱ��f�䣨x��=-$\frac{1}{{x}^{2}}$=-$\frac{1}{3}$��⇒x=$\sqrt{3}$����
���ڢۣ�����ͼ�ο��жϣ�
���ڢܣ���x�ʣ�0��+�ޣ�ʱ��1��f��x����2�����ж�
��� �⣺����f��x����ͼ����ͼ��ʾ��
���ڢ٣�f��1��=2��f��f��1����=f��2��=$\frac{3}{2}$��f��3��=$\frac{4}{3}$���ʢ���ȷ��
���ڢڣ�x��1ʱ��f�䣨x��=-$\frac{1}{{x}^{2}}$=-$\frac{1}{3}$��⇒x=$\sqrt{3}$���ʢ���ȷ��
���ڢۣ�����ͼ�ο��жϢ���ȷ��
���ڢܣ�x�ʣ�0��+�ޣ�ʱ��1��f��x����2��
��?x1��x2�ʣ�0��+�ޣ���|f��x1��-f��x2��|��1��ȷ
�ʴ�Ϊ���٢ڢۢ�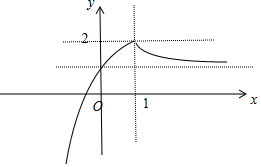
���� ���⿼���˺�����ͼ�������ʣ����ν��˼�롢ת��˼�룬�����е��⣮

��ϰ��ϵ�д�
 ����������ϵ�д�
����������ϵ�д� �Ż���ҵ�Ϻ��Ƽ����׳�����ϵ�д�
�Ż���ҵ�Ϻ��Ƽ����׳�����ϵ�д�
�����Ŀ
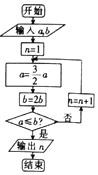
6��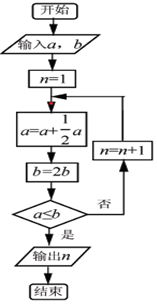 ִ����ͼ��ʾ�ij����ͼ���������a=16��b=4���������n=��������
ִ����ͼ��ʾ�ij����ͼ���������a=16��b=4���������n=��������
 ִ����ͼ��ʾ�ij����ͼ���������a=16��b=4���������n=��������
ִ����ͼ��ʾ�ij����ͼ���������a=16��b=4���������n=��������| A�� | 4 | B�� | 5 | C�� | 6 | D�� | 7 |
7����֪{an}Ϊ�Ȳ����У�SnΪ��ǰn��ͣ���a1=2��S3=15����a6=��������
| A�� | 17 | B�� | 14 | C�� | 13 | D�� | 3 |
11�����к����У�����ż�������ǣ�0��+�ޣ��ϵ����������ǣ�������
| A�� | y=x3 | B�� | y=2|x| | C�� | y=-x2 | D�� | y=log3��-x�� |
8����֪˫����C��$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1��a��0��b��0����һ����������ֱ��l��x-y+2=0ƽ�У���˫����C��������Ϊ��������
| A�� | $\frac{\sqrt{5}}{2}$ | B�� | $\sqrt{2}$ | C�� | $\frac{2\sqrt{3}}{3}$ | D�� | $\sqrt{10}$ |
5����֪��F2��P�ֱ�Ϊ˫����$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1��{a��0��b��0}��$���ҽ�������֧�ϵ�һ�㣬OΪ����ԭ�㣬����M��PF2���е㣬$|{\overrightarrow{O{F_2}}}|=|{\overrightarrow{{F_2}M}}$|����$\overrightarrow{O{F_2}}•\overrightarrow{{F_2}M}=\frac{c^2}{2}$�����˫���ߵ�������Ϊ��������
| A�� | $\frac{{\sqrt{3}+1}}{2}$ | B�� | $\frac{3}{2}$ | C�� | $\sqrt{3}$ | D�� | $2\sqrt{3}$ |

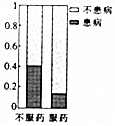
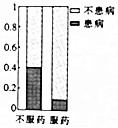
 ��������ѧ���ɡ����������⣺���ɳ���ߣ������ߣ������룬�����Ա���������ն����ȡ�����λ�����˼�ǣ���������߳����������߳�����ÿ������ǰһ�쳤�ȵ�һ�룬��ÿ������ǰһ�쳤�ȵ�����������Ϊ���о�������⣬��a�����ɳ�����b�������������ͼ��ʾ�ij����ͼ�������a��b��ֵ�ֱ�Ϊ5��2���������n��ֵΪ��������
��������ѧ���ɡ����������⣺���ɳ���ߣ������ߣ������룬�����Ա���������ն����ȡ�����λ�����˼�ǣ���������߳����������߳�����ÿ������ǰһ�쳤�ȵ�һ�룬��ÿ������ǰһ�쳤�ȵ�����������Ϊ���о�������⣬��a�����ɳ�����b�������������ͼ��ʾ�ij����ͼ�������a��b��ֵ�ֱ�Ϊ5��2���������n��ֵΪ��������