题目内容
已知f（x）=
，则f[f（-2）]的值为（ ）
|
| A、2 | ||
B、
| ||
| C、-1 | ||
| D、4 |
考点：函数的值
专题：函数的性质及应用
分析：利用分段函数的性质求解．
解答：
解：∵f（x）=
，
∴f（-2）=-2+3=1，
f[f（2）]=f（1）=21=2．
故选：A．
|
∴f（-2）=-2+3=1，
f[f（2）]=f（1）=21=2．
故选：A．
点评：本题考查函数值的求法，是基础题，解题时要注意分段函数的性质的灵活运用．
练习册系列答案
相关题目
如果角α的终边过点（2sin60°，-2cos60°），则sinα的值等于（ ）
A、
| ||||
B、-
| ||||
C、-
| ||||
D、-
|
已知双曲线C：
-
=1的实轴长为2
，右焦点F到渐近线的距离为
，则C的方程为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| 5 |
| 5 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知不等式x2-ax+1＞0对任意x∈[0，2]恒成立，则实数a的取值范围为（ ）
A、（-∞，
| ||
| B、（-2，2） | ||
| C、[-2，2] | ||
| D、（-∞，2） |
| 29π |
| 6 |
| A、第一象限角 |
| B、第二象限角 |
| C、第三象限角 |
| D、第四象限角 |
正整数按下表的规律排列：则上起第2012行左起2013列的数为（ ）
| A、20122 |
| B、20132 |
| C、2011×2012 |
| D、2012×2013 |
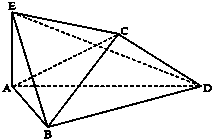菱形ABCD边长为2，∠BAD=60°，将ABCD沿对角线BD折叠，使得平面ABD⊥平面CBD，AE⊥平面ABD，且AE=