题目内容
已知sinα=-
,且α是第四象限角,求tanα[cos(3π-α)-sin(5π+α)]的值.
| 3 |
| 5 |
考点:运用诱导公式化简求值
专题:计算题,三角函数的求值
分析:由已知和同角三角函数关系式可先求得cosα,tanα的值,由诱导公式化简所求后代入即可求值.
解答:
解:∵sinα=-
,且α是第四象限角,
∴cosα=
=
,tanα=
=-
tanα[cos(3π-α)-sin(5π+α)]=tanα×(sinα-cosα)=(-
)×(-
-
)=
.
| 3 |
| 5 |
∴cosα=
| 1-sin2α |
| 4 |
| 5 |
| sinα |
| cosα |
| 3 |
| 4 |
tanα[cos(3π-α)-sin(5π+α)]=tanα×(sinα-cosα)=(-
| 3 |
| 4 |
| 3 |
| 5 |
| 4 |
| 5 |
| 21 |
| 20 |
点评:本题主要考察了同角三角函数关系式,运用诱导公式化简求值,属于基础题.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
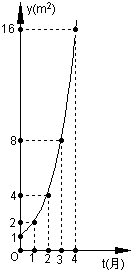 如图是某池塘中的浮萍蔓延的面积y(m2)与时间t(月)的关系:y=at的图象,有以下叙述,其中正确的是( )
如图是某池塘中的浮萍蔓延的面积y(m2)与时间t(月)的关系:y=at的图象,有以下叙述,其中正确的是( )①这个指数函数的底数为2;
②第5个月时,浮萍面积就会超过30m2;
③浮萍每月增加的面积都相等;
④若浮萍蔓延到2m2、3m2、6m2所经过的时间分别为t1,t2,t3,则t1+t2=t3.
| A、①② | B、①②③④ |
| C、②③④ | D、①②④ |
满足loga1(a>0且a≠1)=( )
| A、4 | B、0 | C、2 | D、1 |
已知命题p:“任意x∈R时,都有x2-x+
>0”;命题q:“存在x∈R,使sinx+cosx=
成立”.则下列判断正确的是( )
| 1 |
| 4 |
| 2 |
| A、命题q为假命题 |
| B、命题P为真命题 |
| C、p∧q为真命题 |
| D、p∨q是真命题 |
数列{an}的通项公式an=
,则S5=( )
| 1 |
| n(n+1) |
| A、1 | ||
B、
| ||
C、
| ||
D、
|
 如图,棱长为2的正方体ABCD-A1B1C1D1中,E为棱C1D1上的动点,F为棱BC的中点.
如图,棱长为2的正方体ABCD-A1B1C1D1中,E为棱C1D1上的动点,F为棱BC的中点.