题目内容
已知x+2y+3z=1,则x2+y2+z2取最小值时,x+y+z的值为________.

分析:由柯西不等式可知:(x+2y+3z)2≤(x2+y2+z2)(12+22+32),故x2+y2+z2≥
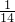 ,当且仅当
,当且仅当  取等号,此时y=2x,z=3x,x+2y+3z=14x=1,由此能求出x+y+z的值.
取等号,此时y=2x,z=3x,x+2y+3z=14x=1,由此能求出x+y+z的值.解答:由柯西不等式可知:(x+2y+3z)2≤(x2+y2+z2)(12+22+32)
故x2+y2+z2≥
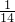 ,当且仅当
,当且仅当  取等号,
取等号,此时y=2x,z=3x,x+2y+3z=14x=1,
∴x=
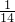 ,y=
,y= ,x=
,x=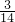 ,
,x+y+z=
 .
.故答案为:
 .
.点评:本题考查柯西不等式的应用,解题时要认真审题,注意x2+y2+z2取最小值时的条件的灵活运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目