题目内容
(不等式选讲选做题)已知x+2y+3z=1,求x2+y2+z2的最小值 .
【答案】分析:解法一:利用柯西不等式即可得出.
解法二:利用向量的数量积的性质即可得出.
解答:解:解法一:由柯西不等式可知:(x+2y+3z)2≤(x2+y2+z2)(12+22+33),
∴ ,
,
当且仅当 ,x+2y+3z=1,即
,x+2y+3z=1,即 ,
, ,
, 时取等号.
时取等号.
即x2+y2+z2的最小值为 .
.
解法二:设向量 ,
, ,
,
∵ ,∴1=x+2y+3z≤
,∴1=x+2y+3z≤ ,
,
∴ ,当且仅当
,当且仅当 与
与 共线时取等号,即
共线时取等号,即 ,x+2y+3z=1,解得
,x+2y+3z=1,解得 ,
, ,
, 时取等号.
时取等号.
故答案为 .
.
点评:熟练掌握向量的数量积的性质和正确理解柯西不等式是解题的关键.
解法二:利用向量的数量积的性质即可得出.
解答:解:解法一:由柯西不等式可知:(x+2y+3z)2≤(x2+y2+z2)(12+22+33),
∴
 ,
,当且仅当
 ,x+2y+3z=1,即
,x+2y+3z=1,即 ,
, ,
, 时取等号.
时取等号.即x2+y2+z2的最小值为
 .
.解法二:设向量
 ,
, ,
,∵
 ,∴1=x+2y+3z≤
,∴1=x+2y+3z≤ ,
,∴
 ,当且仅当
,当且仅当 与
与 共线时取等号,即
共线时取等号,即 ,x+2y+3z=1,解得
,x+2y+3z=1,解得 ,
, ,
, 时取等号.
时取等号.故答案为
 .
.点评:熟练掌握向量的数量积的性质和正确理解柯西不等式是解题的关键.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
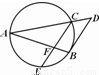
 ,则线段CD的长为 .
,则线段CD的长为 .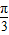 )的直角坐标是 .
)的直角坐标是 .
 ,则线段CD的长为 .
,则线段CD的长为 . )的直角坐标是 .
)的直角坐标是 .
 ,则线段CD的长为 .
,则线段CD的长为 . )的直角坐标是 .
)的直角坐标是 .
 ,则线段CD的长为 .
,则线段CD的长为 .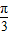 )的直角坐标是 .
)的直角坐标是 .
 ,则线段CD的长为 .
,则线段CD的长为 . )的直角坐标是 .
)的直角坐标是 .