题目内容
已知f(x)=3x2-x+m,(x∈R),g(x)=ln x.
(1)若函数f(x)与g(x)的图像在x=x0处的切线平行,求x0的值;
(2)求当曲线y=f(x)与y=g(x)有公共切线时,实数m的取值范围;
(3)在(2)的条件下,求函数F(x)=f(x)-g(x)在区间 上的最值(用m表示).
上的最值(用m表示).
解:(1)∵f′(x)=6x-1,g′(x)= (x>0),
(x>0),
由题意知6x0-1= (x0>0),即6x
(x0>0),即6x -x0-1=0,解得x0=
-x0-1=0,解得x0=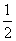 或x0=-
或x0=-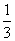 ,
,
又∵x0>0,∴x0=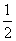 .
.
(2)若曲线y=f(x)与y=g(x)相切且在交点处有公共切线,由(1)得切点横坐标为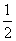 ,
,
∴f =g
=g ,
,
∴ -
-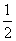 +m=ln
+m=ln 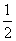 ,即m=-
,即m=- -ln 2,
-ln 2,

数形结合可知,m>- -ln 2时,f(x)与g(x)有公共切线,故m的取值范围是
-ln 2时,f(x)与g(x)有公共切线,故m的取值范围是
 (3)F(x)=f(x)-g(x)=3x2-x+m-ln x,
(3)F(x)=f(x)-g(x)=3x2-x+m-ln x,
故F′(x)=6x-1-
 当x变化时,F′(x)与F(x)在区间
当x变化时,F′(x)与F(x)在区间
 的变化情况如下表:
的变化情况如下表:



练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,函数g(x)=
,函数g(x)= 则函数g(x)的最小值是________.
则函数g(x)的最小值是________.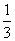 x3-
x3- x2-40x(x>0),为使耗电量最小,则速度应定为________.
x2-40x(x>0),为使耗电量最小,则速度应定为________. B.
B. 
 ,且α∈
,且α∈ ,则tan(2π-α)的值为________.
,则tan(2π-α)的值为________. 对应的向量分别是
对应的向量分别是 则
则 =( )
=( ) D.
D. 
