题目内容
已知函数f(x)=ax+x2-xln a-b(a,b∈R,a>1),e是自然对数的底数.
(1)试判断函数f(x)在区间(0,+∞)上的单调性;
(2)当a=e,b=4时,求整数k的值,使得函数f(x)在区间(k,k+1)上存在零点.
解:(1)f′(x)=axln a+2x-ln a=2x+(ax-1)ln a.
∵a>1,∴当x∈(0,+∞)时,ln a>0,
ax-1>0,
∴f′(x)>0,
∴函数f(x)在(0,+∞)上单调递增.
(2)∵f(x)=ex+x2-x-4,∴f′(x)=ex+2x-1,∴f′(0)=0,当x>0时,ex>1,
∴f′(x)>0,
∴f(x)是(0,+∞)上的增函数;
同理,f(x)是(-∞,0)上的减函数.
又f(0)=-3<0,f(1)=e-4<0,
f(2)=e2-2>0,当x>2时,f(x)>0,
∴当x>0时,函数f(x)的零点在(1,2)内,
∴k=1满足条件;
f(0)=-3<0,f(-1)= -2<0,
-2<0,
f(-2)= +2>0,当x<-2时,f(x)>0,
+2>0,当x<-2时,f(x)>0,
∴当x<0时,函数f(x)的零点在(-2,-1)内,∴k=-2满足条件.
综上所述,k=1或-2.

练习册系列答案
相关题目
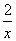 ,g(x)=a(2-ln x)(a>0).若曲线y=f(x)与曲线y=g(x)在x=1处的切线斜率相同,求a的值,并判断两条切线是否为同一条直线.
,g(x)=a(2-ln x)(a>0).若曲线y=f(x)与曲线y=g(x)在x=1处的切线斜率相同,求a的值,并判断两条切线是否为同一条直线.
 上的最值(用m表示).
上的最值(用m表示). ,1),将点A绕O逆时针旋转90°到B点,则B点坐标为__________.
,1),将点A绕O逆时针旋转90°到B点,则B点坐标为__________. B.
B.