题目内容
已知椭圆 .
.
(Ⅰ)求 的离心率及长轴长;
的离心率及长轴长;
(Ⅱ)设过椭圆 的上顶点
的上顶点 的直线
的直线 与椭圆
与椭圆 的另一个交点为
的另一个交点为 ,线段
,线段 的垂直平分线交椭圆
的垂直平分线交椭圆 于
于 两点. 问:是否存在直线
两点. 问:是否存在直线 使得
使得 三点共线(
三点共线( 为坐标原点)?若存在,求出所有满足条件的直线
为坐标原点)?若存在,求出所有满足条件的直线 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
解:(Ⅰ)由题意可知椭圆 的标准方程为:
的标准方程为: ,则
,则 .
.
所以 椭圆 的长轴长为
的长轴长为 .
.
因为  ,
,
所以  ,即
,即 的离心率为
的离心率为 .
.
(Ⅱ)若 三点共线,由
三点共线,由 是线段
是线段 的垂直平分线可得:
的垂直平分线可得:
 .
.
由(Ⅰ)可得 ,设
,设 .
.
所以  . ①
. ①
又因为  , ②
, ②
由①②可得:  (舍),或
(舍),或
当 时,直线
时,直线 的方程为
的方程为 ,显然满足题意.
,显然满足题意.
所以 存在直线 使得
使得 三点共线,直线
三点共线,直线 的方程为
的方程为 .
.

练习册系列答案
相关题目
 ,圆心角为
,圆心角为 的扇形,则此圆锥的体积为 .
的扇形,则此圆锥的体积为 .  的值是________.
的值是________.
 . 命题
. 命题
 ,函数
,函数 是偶函数;命题
是偶函数;命题
 ,函数
,函数



 中,若
中,若 ,
, ,则公比
,则公比 ________;当
________;当 ________时,
________时,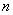 项积最大.
项积最大.  上随机取一个数
上随机取一个数 ,则
,则 的概率为 ( )
的概率为 ( )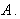

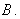



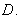

 都是定义在
都是定义在 上的函数,
上的函数, ,
, ,且
,且
 ,且
,且 ,
, .若数列
.若数列 的前
的前 项和大于
项和大于 ,
, 表示的曲线是( )
表示的曲线是( )