题目内容
若曲线y=k|x|与y=x+k(k＞0)有两个公共点,求k的取值范围.
解:由
可得k|x|=x+k. ①
若x≥0,则方程①可化为kx=x+k,
当k=1时,x=x+1不成立.
∴x=
≥0.
若x＜0,则方程①可化为-kx=x+k,
∴x=-
＜0.
于是应有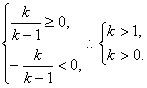
∴k＞1,即所求的k的取值范围为(1,+∞).
练习册系列答案
活力课时同步练习册系列答案
相关题目
活力课时同步练习册系列答案题目内容
若曲线y=k|x|与y=x+k(k＞0)有两个公共点,求k的取值范围.
解:由
可得k|x|=x+k. ①
若x≥0,则方程①可化为kx=x+k,
当k=1时,x=x+1不成立.
∴x=≥0.
若x＜0,则方程①可化为-kx=x+k,
∴x=-＜0.
于是应有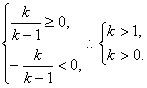
∴k＞1,即所求的k的取值范围为(1,+∞).
活力课时同步练习册系列答案
y=x+2垂直，求函数y=f(x)的单调区间；[来源:学&科&网Z&X&X&K]
成立，试求a的取值范围；
上有两个零点，求实数b的取值范围。
R.
，比较
与
的大小并说明理由。
成立，试求a的取值范围；
上有两个零点，求实数b的取值范围。