Question

（本小题满分12分）
已知函数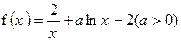
（Ⅰ）若曲线y=f(x)在点P（1，f(1)）处的切线与直线y=x+2垂直，求函数y=f(x)的单调区间；[来源:学&科&网Z&X&X&K]
（Ⅱ）若对于任意成立，试求a的取值范围；
（Ⅲ）记g(x)=f(x)+x-b(b∈R).当a=1时，函数g(x)在区间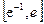上有两个零点，求实数b的取值范围。

Answer 1

解：（Ⅰ）直线y=x+2的斜率为1， 函数f(x)的定义域为  
因为，所以，所以a=1
所以
由解得x>2 ; 由解得0<x<2
所以f(x)得单调增区间是，单调减区间是 ………………………4分
（Ⅱ）
由解得由解得
所以f(x)在区间上单调递增，在区间上单调递减
所以当时，函数f(x)取得最小值
因为对于任意成立，
所以即可
则，由解得
所以a得取值范围是     …………………………… 8分
（Ⅲ）依题意得，则
由解得x>1，由解得0<x<1
所以函数g(x)在区间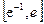上有两个零点，
所以     解得
所以b得取值范围是    ………………………………  12分

解析