Question

己知函数f(x)=e^x，x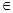R.

(1)若直线y=kx+1与f(x)的反函数图象相切，求实数k的值；

(2)设x﹥0，讨论曲线y=f(x)与曲线y=mx²(m﹥0)公共点的个数；

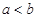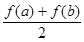(3)设，比较与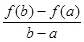的大小并说明理由。

 

Answer 1

【答案】

(1)；(2)当m时,有0个公共点;当m=,有1个公共点;当m有2个公共点；(3).

【解析】

试题分析：(1)f (x)的反函数. 直线y=kx+1恒过点P（0，1），该题即为过某点与曲线相切的问题，这类题一定要先设出切点的坐标，然后求导便可得方程组，解方程组即可得k的值.

 (2)曲线y=f(x)与曲线 的公共点个数即方程 根的个数. 而这个方程可化为

，令，结合的图象即可知道取不同值时，方程的根的个数.

(3) 比较两个式子的大小的一般方法是用比较法，即作差，变形，判断符号.

 

 

结合这个式子的特征可看出，我们可研究函数的函数值的符号，而用导数即可解决.

试题解析：(1)f(x)的反函数.设直线y=kx+1与相切于点，则.所以                       4分

(2)当x>0,m>0时,曲线y=f(x)与曲线的公共点个数即方程根的个数. 5分

由，令，

则 在上单调递减，这时；  在上单调递增，这时；所以是的最小值.      6分

所以对曲线y=f(x)与曲线公共点的个数,讨论如下:

当m时,有0个公共点;

当m=,有1个公共点;

当m有2个公共点;                  8分

(3)设 

           9分

令，则，

的导函数，所以在上单调递增，且，因此，在上单调递增，而，所以在上.   12分

当时，且即，

 

所以当时，                     14分

考点：1、导数的应用；2、方程的根；3、比较大小.