题目内容
18. 如图,在直三棱柱ABC-A1B1C1中,△ABC是等腰直角三角形,AC=BC=AA1=2,D为侧棱AA1的中点;
如图,在直三棱柱ABC-A1B1C1中,△ABC是等腰直角三角形,AC=BC=AA1=2,D为侧棱AA1的中点;(1)求证:AC⊥平面BCC1B1;
(2)求异面直线B1D与AC所成角的大小.
分析 (1)由已知推导出AC⊥BC,CC1⊥AC,由此能证明AC⊥平面BCC1B1.
(2)以C为原点,直线CA、CB、CC1为x、y、z轴,建立空间直角坐标系,利用向量法能求出异面直线B1D与AC所成角的大小.
解答 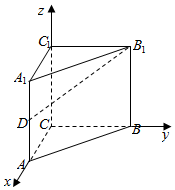 证明:(1)∵底面△ABC是等腰直角三角形,且AC=BC,
证明:(1)∵底面△ABC是等腰直角三角形,且AC=BC,
∴AC⊥BC,
∵CC1⊥平面A1B1C1,∴CC1⊥AC,
∵CC1∩BC=C,∴AC⊥平面BCC1B1.
解:(2)以C为原点,直线CA、CB、CC1为x、y、z轴,建立空间直角坐标系,
则C(0,0,0),A(2,0,0),B(0,2,0),C1(0,0,2),B1(0,2,2),D(2,0,1),
$\overrightarrow{{B}_{1}D}$=(2,-2,-1),$\overrightarrow{AC}$=(-2,0,0),
设异面直线B1D与AC所成角为θ,
则cosθ=$\frac{|\overrightarrow{AC}•\overrightarrow{B{D}_{1}}|}{|\overrightarrow{AC}|•|\overrightarrow{{B}_{1}D}|}$=$\frac{|-4|}{\sqrt{9}•2}$=$\frac{2}{3}$.
∴$θ=arccos\frac{2}{3}$.
∴异面直线B1D与AC所成角的大小为arccos$\frac{2}{3}$.
点评 本题考查线面垂直的证明,考查异面直线所成角的求法,是中档题,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
3.有一个容量为60的样本,数据的分组及各组的频数如下:
[11.5,15.5)2;
[15.5,19.5)4;
[19.5,23.5)5;
[23.5,27.5)16;
[27.5,31.5)1l;
[31.5,35.5)12;
[35.5.39.5)7;
[39.5,43.5)3;
根据样本的频率分布估计,数据落在[27.5,39.5)的概率约是( )
[11.5,15.5)2;
[15.5,19.5)4;
[19.5,23.5)5;
[23.5,27.5)16;
[27.5,31.5)1l;
[31.5,35.5)12;
[35.5.39.5)7;
[39.5,43.5)3;
根据样本的频率分布估计,数据落在[27.5,39.5)的概率约是( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
7.若函数f(x)=sin(ωx+$\frac{π}{6}$)-cosωx的图象相邻两个对称中心之间的距离为$\frac{π}{2}$,则f(x)的一个单调增区间为( )
| A. | (-$\frac{π}{6}$,$\frac{π}{3}$) | B. | (-$\frac{π}{3}$,$\frac{π}{6}$) | C. | ($\frac{π}{6}$,$\frac{2π}{3}$) | D. | ($\frac{π}{3}$,$\frac{5π}{6}$) |
8.复数Z=$\frac{2+ai}{1+i}$(a∈R)在复平面内对应的点在虚轴上,则a=( )
| A. | 2 | B. | -2 | C. | 1 | D. | -1 |