题目内容
12.若P是椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1上位于x轴上方的一点,F是椭圆的左焦点,O为原点,Q为PF的中点,且|OQ|=4,则直线PF的斜率为$\sqrt{63}$.分析 设椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1的右焦点为E,由已知推导出PE=8,PF=2,EF=8,利用余弦定理求出cos∠PFE,由此能求出直线PF的斜率.
解答 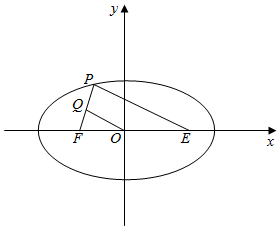 解:如图,设椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1的右焦点为E
解:如图,设椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1的右焦点为E
∵P是椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1上位于x轴上方的一点,F是椭圆的左焦点,O为原点,Q为PF的中点,且|OQ|=4,
∴OQ是△PEF的中位线,∴PE=2OQ=8,
∴PF=2a-8=2×5=8=2,EF=2c=8,
∴cos∠PFE=$\frac{P{F}^{2}+E{F}^{2}-P{E}^{2}}{2PF•EF}$=$\frac{4+64-64}{2×2×8}$=$\frac{1}{8}$,
∴sin∠PFE=$\sqrt{1-\frac{1}{64}}$=$\frac{\sqrt{63}}{8}$,∴tan∠PFE=$\sqrt{63}$.
∴直线PF的斜率为$\sqrt{63}$.
故答案为:$\sqrt{63}$.
点评 本题考查直线的斜率的求法,是中档题,解题时要认真审题,注意椭圆性质的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2.已知向量$\overrightarrow{a}$=(cosα,sinβ),$\overrightarrow{b}$=(sinα,cosβ),若$\overrightarrow{a}$∥$\overrightarrow{b}$,则α,β的值可以是( )
| A. | α=$\frac{π}{3}$,β=-$\frac{π}{3}$ | B. | α=$\frac{π}{3}$,β=$\frac{2π}{3}$ | C. | α=$\frac{π}{5}$,β=-$\frac{7π}{10}$ | D. | α=$\frac{π}{3}$,β=-$\frac{π}{6}$ |
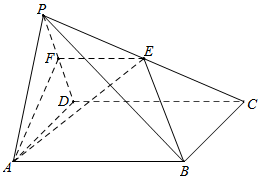 如图,在四棱锥P-ABCD中,底面ABCD是正方形.点E是棱PC的中点,平面ABE与棱PD交于点F.
如图,在四棱锥P-ABCD中,底面ABCD是正方形.点E是棱PC的中点,平面ABE与棱PD交于点F. 如图是根据某中学为地震灾区捐款的情况而制作的统计图,已知该校在校学生3000人,根据统计图计算该校共捐款37770元.
如图是根据某中学为地震灾区捐款的情况而制作的统计图,已知该校在校学生3000人,根据统计图计算该校共捐款37770元.