题目内容
7.已知函数f(x)=|x+1|-2|x-a|,a∈R,若f(x)的图象与x轴围成的三角形面积大于6,求a的取值范围.分析 化为分段函数可得三个交点,由面积公式可得a的不等式,解不等式可得.
解答 解:若a>-1,则f(x)=$\left\{\begin{array}{l}{x-1-2a,x<-1}\\{3x+1-2a,-1≤x≤a}\\{-x+1+2a,x>a}\end{array}\right.$,
∴函数f(x)的图象与x轴围成的三角形的三个顶点分别为A($\frac{2a-1}{3}$,0),B(2a+1,0),C(a,a+1),
∴△ABC的面积S=$\frac{1}{2}$[2a+1-($\frac{2a-1}{3}$)](a+1)=$\frac{2}{3}$(a+1)2,故$\frac{2}{3}$(a+1)2>6,解得a>2或a<-4(舍),
若a=-1,则f(x)=|x+1|-2|x+1|=-|x+1|,此时不满足条件.
若a<-1,则f(x)=$\left\{\begin{array}{l}{x-1-2a,}&{x<a}\\{-3x+2a-1,}&{a≤x≤-1}\\{-x+1+2a,}&{x>-1}\end{array}\right.$,
函数f(x)的图象与x轴围成的三角形的三个顶点分别为A($\frac{2a-1}{3}$,0),B(2a+1,0),C(a,-a-1),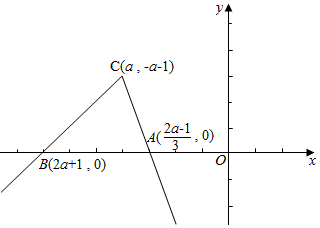
∴△ABC的面积S=$\frac{1}{2}$[$\frac{2a-1}{3}$-(2a+1)](-a-1)=$\frac{2}{3}$(a+1)2,故$\frac{2}{3}$(a+1)2>6,解得a>2(舍)或x<-4,
综上a的取值范围为(-∞,-4)∪(2,+∞).
点评 本题考查绝对值函数,涉及三角形的公式,化为分段函数是解决问题的关键,注意要对a进行分类讨论.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17. 某学校为了宣传环保知识,举办了“环保知识竞赛”活动
某学校为了宣传环保知识,举办了“环保知识竞赛”活动
(1)若从全校高一至高三的学生答卷中抽取了100份,成绩统计结果如表所示,分别求出n,a,b的值;
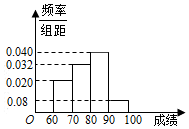
(2)若对高一年级1000名学生的成绩进行统计,结果为如图频率分布直方图;若成绩在90分以上的同学授予“环保之星”,从成绩在[60,70]和(90,100]的同学中按分层抽样的方法选出7人,求从这7人中随机抽取2人,恰有1人是“环保之星”的概率.
 某学校为了宣传环保知识,举办了“环保知识竞赛”活动
某学校为了宣传环保知识,举办了“环保知识竞赛”活动(1)若从全校高一至高三的学生答卷中抽取了100份,成绩统计结果如表所示,分别求出n,a,b的值;
| 年级 | 抽取份数 | 优秀人数 | 优秀率 |
| 高一 | 40 | a | 0.5 |
| 高二 | n | 18 | 0.6 |
| 高三 | 30 | 21 | b |
15.已知A,B,C,D是复平面内的四个不同点,点A,B,C对应的复数分别是1+3i,-i,2+i,若$\overrightarrow{AD}=\overrightarrow{BC}$,则点D表示的复数是( )
| A. | 1-3i | B. | -3-i | C. | 3+5i | D. | 5+3i |
17.已知函数f(x)为偶函数,且当x≤0时,f(x)=$\frac{10+3x+{2}^{-x}}{7}$+|$\frac{10+3x-{2}^{-x}}{7}$|+m,若函数f(x)有4个零点,则实数m的取值范围为( )
| A. | (-$\frac{20}{7}$,-$\frac{8}{7}$) | B. | (-∞,-3)∪(-$\frac{8}{7}$,+∞) | C. | (-2,-$\frac{10}{7}$) | D. | (-∞,-2)∪(-$\frac{10}{7}$,+∞) |
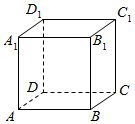 (普通中学做)ABCD-A1B1C1D1是棱长为1的正方体,一个质点从A出发沿正方体的面对角线运动,每走完一条面对角线称为“走完一段”,质点的运动规则如下:运动第i段与第i+2所在直线必须是异面直线(其中i是正整数).问质点从A点出发又回到起点A走完的段数是( )
(普通中学做)ABCD-A1B1C1D1是棱长为1的正方体,一个质点从A出发沿正方体的面对角线运动,每走完一条面对角线称为“走完一段”,质点的运动规则如下:运动第i段与第i+2所在直线必须是异面直线(其中i是正整数).问质点从A点出发又回到起点A走完的段数是( )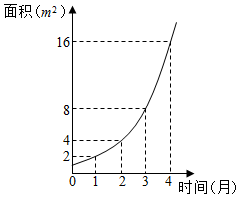 最近几年,每年11月初,黄浦江上漂浮着的水葫芦便会迅速增长,严重影响了市容景观,为了解决这个环境问题,科研人员进行科研攻关,如图是科研人员在实验室池塘中观察水葫芦面积与时间的函数关系图象,假设其函数关系为指数函数,并给出下列说法:
最近几年,每年11月初,黄浦江上漂浮着的水葫芦便会迅速增长,严重影响了市容景观,为了解决这个环境问题,科研人员进行科研攻关,如图是科研人员在实验室池塘中观察水葫芦面积与时间的函数关系图象,假设其函数关系为指数函数,并给出下列说法: