Question

四棱锥A-BCDE中，AD=

1

2

AE，二面角A-DE-B成直二面角，∠DBC=∠DAE=60°，AD=1．
（Ⅰ）求证：AD⊥平面BCED；
（Ⅱ）若BD⊥AC，平面ABC与平面BCD所成的角为30°，求三棱锥A-BCD的体积V．

Answer 1

考点：直线与平面垂直的判定,棱柱、棱锥、棱台的体积

专题：空间位置关系与距离

分析：（Ⅰ）取AE的中点F，由已知得△ADF是等边三角形，从而AD⊥DE，由此能证明AD⊥平面BCED．
（Ⅱ）作DG⊥BC于G，连结AG，由三垂直线定理，得AG⊥BC，从而∠AGB就是AG与面BCD所成的角，由此能求出三棱锥A-BCD的体积．

解答： （Ⅰ）证明：取AE的中点F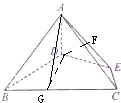，∵四棱锥A-BCDE中，AD=

1

2

AE，∠DBC=∠DAE=60°，
∴△ADF是等边三角形，
∴DF=AF=EF=

1

2

AE，∴AD⊥DE，
又面ADE⊥面BCED，
∴AD⊥平面BCED．
（Ⅱ）解：作DG⊥BC于G，连结AG，
由三垂直线定理，得AG⊥BC，
∴∠AGB就是AG与面BCD所成的角，
∵BD⊥AD，BD⊥AC，
∴BD⊥DC，
Rt△ADG中，DG=

3

，
Rt△BGD中，BD=2，
Rt△BDC中，DC=2

3

，
∴三棱锥A-BCD的体积V=

1

3

×

1

2

×2×2

3

×1=

2 3

3

．

点评：本题考查直线与平面垂直的证明，考查三棱锥的体积的求法，解题时要认真审题，注意空间思维能力的培养．